题目内容
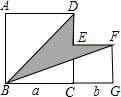 如图,两个正方形边长分别为a、b,如果a+b=17,ab=60,求阴影部分的面积.
如图,两个正方形边长分别为a、b,如果a+b=17,ab=60,求阴影部分的面积.分析:阴影部分的面积=正方形ABCD的面积+正方形EFGC的面积-三角形ABD的面积-三角形BGF的面积,列出关系式,整理后,将a+b及ab的值代入,即可求出阴影部分的面积.
解答:解:∵a+b=17,ab=60,
∴S阴影=S正方形ABCD+S正方形EFGC-S△ABD-S△BGF
=a2+b2-
a2-
(a+b)•b=a2+b2-
a2-
ab-
b2=
a2+
b2-
ab
=
(a2+b2-ab)=
[(a+b)2-3ab]=
×(172-3×60)=
.
∴S阴影=S正方形ABCD+S正方形EFGC-S△ABD-S△BGF
=a2+b2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 109 |
| 2 |
点评:此题考查了整式混合运算的应用,弄清题意列出阴影部分的面积是解本题的关键.

练习册系列答案
相关题目
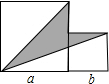 如图,两个正方形边长分别为a、b,
如图,两个正方形边长分别为a、b,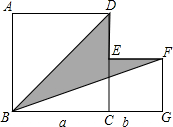 如图,两个正方形边长分别为a、b,如果a+b=17,ab=60,则阴影部分的面积为
如图,两个正方形边长分别为a、b,如果a+b=17,ab=60,则阴影部分的面积为 如图,两个正方形边长分别为a、b,
如图,两个正方形边长分别为a、b, 如图,两个正方形边长分别为a、b,如果a+b=17,ab=60,求阴影部分的面积.
如图,两个正方形边长分别为a、b,如果a+b=17,ab=60,求阴影部分的面积.