题目内容
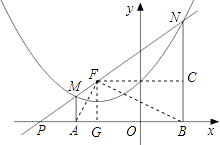
【题目】抛物线y= ![]() +x+m的顶点在直线y=x+3上,过点F(﹣2,2)的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.
+x+m的顶点在直线y=x+3上,过点F(﹣2,2)的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.
(1)先通过配方求抛物线的顶点坐标(坐标可用含m的代数式表示),再求m的值;
(2)设点N的横坐标为a,试用含a的代数式表示点N的纵坐标,并说明NF=NB;
(3)若射线NM交x轴于点P,且PAPB= ![]() ,求点M的坐标.
,求点M的坐标.
【答案】
(1)
解:y= ![]() x2+x+m=
x2+x+m= ![]() (x+2)2+(m﹣1)
(x+2)2+(m﹣1)
∴顶点坐标为(﹣2,m﹣1)
∵顶点在直线y=x+3上,
∴﹣2+3=m﹣1,
得m=2
(2)
解:过点F作FC⊥NB于点C,
∵点N在抛物线上,
∴点N的纵坐标为: ![]() a2+a+2,
a2+a+2,
即点N(a, ![]() a2+a+2)
a2+a+2)
在Rt△FCN中,FC=a+2,NC=NB﹣CB= ![]() a2+a,
a2+a,
∴NF2=NC2+FC2=( ![]() a2+a)2+(a+2)2,
a2+a)2+(a+2)2,
=( ![]() a2+a)2+(a2+4a)+4,
a2+a)2+(a2+4a)+4,
而NB2=( ![]() a2+a+2)2,
a2+a+2)2,
=( ![]() a2+a)2+(a2+4a)+4
a2+a)2+(a2+4a)+4
∴NF2=NB2,
NF=NB
(3)
解:连接AF、BF,
由NF=NB,得∠NFB=∠NBF,由(2)的思路知,MF=MA,
∴∠MAF=∠MFA,
∵MA⊥x轴,NB⊥x轴,
∴MA∥NB,
∴∠AMF+∠BNF=180°
∵△MAF和△NFB的内角总和为360°,
∴2∠MAF+2∠NBF=180°,∠MAF+∠NBF=90°,
∵∠MAB+∠NBA=180°,
∴∠FBA+∠FAB=90°,
又∵∠FAB+∠MAF=90°,
∴∠FBA=∠MAF=∠MFA,
又∵∠FPA=∠BPF,
∴△PFA∽△PBF,
∴ ![]() ,PF2=PA×PB=
,PF2=PA×PB= ![]() ,
,
过点F作FG⊥x轴于点G,在Rt△PFG中,
PG= ![]() =
= ![]() ,
,
∴PO=PG+GO= ![]() ,
,
∴P(﹣ ![]() ,0)
,0)
设直线PF:y=kx+b,把点F(﹣2,2)、点P(﹣ ![]() ,0)代入y=kx+b,
,0)代入y=kx+b,
解得k= ![]() ,b=
,b= ![]() ,
,
∴直线PF:y= ![]() x+
x+ ![]() ,
,
解方程 ![]() x2+x+2=
x2+x+2= ![]() x+
x+ ![]() ,
,
得x=﹣3或x=2(不合题意,舍去),
当x=﹣3时,y= ![]() ,
,
∴M(﹣3, ![]() ).
).
【解析】(1)利用配方法将二次函数整理成顶点式即可,再利用点在直线上的性质得出答案即可;(2)首先利用点N在抛物线上,得出N点坐标,再利用勾股定理得出NF2=NC2+FC2 , 进而得出NF2=NB2 , 即可得出答案;(3)求点M的坐标,需要先求出直线PF的解析式.首先由(2)的思路得出MF=MA,然后连接AF、FB,通过证明△PFA∽△PBF,利用相关的比例线段将PAPB的值转化为PF的值,进而求出点F的坐标和直线PF的解析式,即可得解.