题目内容
(2006•襄阳)已知:AC是⊙O的直径,点A、B、C、O在⊙O1上,OA=2.建立如图所示的直角坐标系.∠ACO=∠ACB=60度.(1)求点B关于x轴对称的点D的坐标;
(2)求经过三点A、B、O的二次函数的解析式;
(3)该抛物线上是否存在点P,使四边形PABO为梯形?若存在,请求出P点的坐标;若不存在,请说明理由.

【答案】分析:(1)根据圆的圆周角的性质可求得△AOB是等边三角形,根据等边三角形的性质即可求得点B的坐标,再根据点B关于x轴的对称点的特点求得点D的坐标;
(2)可设得二次函数的一般式,将点A、O、B的坐标代入函数解析式,解方程组即可求得函数的解析式;
(3)∵△BOA是等边三角形,点D是点B关于x轴的对称点
∴OA、BD相互垂直平分∴四边形DABO是菱形
∴AD∥BO∴所求点P必在直线AD上
设直线AD的解析式为y=kx+b(k≠O),利用待定系数法求解即可.
解答: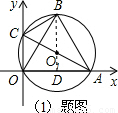 解:(1)如图:∵点A、B、C、D在⊙O上,且∠ACO=∠ACB=60°,
解:(1)如图:∵点A、B、C、D在⊙O上,且∠ACO=∠ACB=60°,
∴∠BOA=∠ABO=60°,
∴△ABO是等边三角形,
∵OA=2,
过点B作BD⊥OA于点D,
∴OD= OA-1,BD=OB•sin60°=
OA-1,BD=OB•sin60°= ,
,
∴B(1,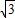 ),
),
∴点B关于x轴对称的点D的坐标为(1,- );
);
(2)设经过A(2,0)、B(1, )、O(0,0)的二次函数的解析式为y=ax2+bx+c(a≠0),
)、O(0,0)的二次函数的解析式为y=ax2+bx+c(a≠0),
∴ ,
,
 ,
,
∴y=- +2
+2 ;
;
(3)存在点P,使四边形PABO为梯形,
∵△BOA是等边三角形,
点D是点B关于x轴的对称点,
∴OA、BD相互垂直平分,
∴四边形DABO是菱形,
∴AD∥BO,
∴所求点P必在直线AD上,
设直线AD的解析式为y=kx+b(k≠O),
∴ ,
,
即 ,
,
∴y= ,
,
联立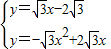 ,
,
解得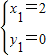
 ,
,
当 时,就是点A(2,0);
时,就是点A(2,0);
当 时,
时,
即为所求点P(-1,-3 ),
),
过点P作PG⊥x轴于G,则|PG|=3 ,
,
∴PA=6而BO=2,
在四边形PABO中,BO∥AP且BO≠AP,
∴四边形PABO不是平行四边形,
∴OP与AB不平行,
∴四边形PABO为梯形,
同理,在抛物线上可求得另一点P(3,-3 ),也能使四边形PABO为梯形.
),也能使四边形PABO为梯形.
故存在点P(-1,-3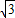 ),或P(3,-3
),或P(3,-3 ),使四边形PABO为梯形.
),使四边形PABO为梯形.
点评:此题考查了二次函数与园的知识的综合应用,解题时要注意待定系数法的应用,还要注意数形结合思想的应用.
(2)可设得二次函数的一般式,将点A、O、B的坐标代入函数解析式,解方程组即可求得函数的解析式;
(3)∵△BOA是等边三角形,点D是点B关于x轴的对称点
∴OA、BD相互垂直平分∴四边形DABO是菱形
∴AD∥BO∴所求点P必在直线AD上
设直线AD的解析式为y=kx+b(k≠O),利用待定系数法求解即可.
解答:
 解:(1)如图:∵点A、B、C、D在⊙O上,且∠ACO=∠ACB=60°,
解:(1)如图:∵点A、B、C、D在⊙O上,且∠ACO=∠ACB=60°,∴∠BOA=∠ABO=60°,
∴△ABO是等边三角形,
∵OA=2,
过点B作BD⊥OA于点D,
∴OD=
 OA-1,BD=OB•sin60°=
OA-1,BD=OB•sin60°= ,
,∴B(1,
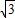 ),
),∴点B关于x轴对称的点D的坐标为(1,-
 );
);(2)设经过A(2,0)、B(1,
 )、O(0,0)的二次函数的解析式为y=ax2+bx+c(a≠0),
)、O(0,0)的二次函数的解析式为y=ax2+bx+c(a≠0),∴
 ,
, ,
,∴y=-
 +2
+2 ;
;(3)存在点P,使四边形PABO为梯形,
∵△BOA是等边三角形,

点D是点B关于x轴的对称点,
∴OA、BD相互垂直平分,
∴四边形DABO是菱形,
∴AD∥BO,
∴所求点P必在直线AD上,
设直线AD的解析式为y=kx+b(k≠O),
∴
 ,
,即
 ,
,∴y=
 ,
,联立
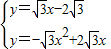 ,
,解得
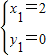
 ,
,当
 时,就是点A(2,0);
时,就是点A(2,0);当
 时,
时,即为所求点P(-1,-3
 ),
),过点P作PG⊥x轴于G,则|PG|=3
 ,
,∴PA=6而BO=2,
在四边形PABO中,BO∥AP且BO≠AP,
∴四边形PABO不是平行四边形,
∴OP与AB不平行,
∴四边形PABO为梯形,
同理,在抛物线上可求得另一点P(3,-3
 ),也能使四边形PABO为梯形.
),也能使四边形PABO为梯形.故存在点P(-1,-3
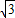 ),或P(3,-3
),或P(3,-3 ),使四边形PABO为梯形.
),使四边形PABO为梯形.点评:此题考查了二次函数与园的知识的综合应用,解题时要注意待定系数法的应用,还要注意数形结合思想的应用.

练习册系列答案
相关题目

 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由. 的值;②求阴影部分的面积.
的值;②求阴影部分的面积.
