题目内容
(2006•襄阳)已知:AB是⊙O的直径,点C是⊙O外的一点,点E是AC上一点,AB=2.(1)如图1,点D是BC的中点,当DE也AC满足什么关系时,DE是⊙O的切线?请说明理由.
(2)如图2,AC是⊙O的切线,点E是AC的中点DE∥AB.①求
 的值;②求阴影部分的面积.
的值;②求阴影部分的面积.
【答案】分析:(1)若DE是圆的切线,则连接OD,OD应垂直于DE,再根据三角形的中位线定理得到OD∥AC,所以DE⊥AC,反之成立;
(2)①中,连接OD,根据平行线等分线段定理,得到D是BC的中点,根据平行线的性质和切线的性质得到DE⊥AC,结合(1)的结论,则DE也是圆的切线,从而得到OD⊥DE,根据一组邻边相等的矩形是正方形得到正方形AEDO,从而发现等腰直角三角形AOD和ADB,根据AB=2,即可求得AD的长,进一步计算;
②中,阴影部分的面积显然是正方形AEDO的面积减去扇形OAD的面积,根据①中的结论即可计算.
解答: 解:(1)如图所示,
解:(1)如图所示,
当DE⊥AC时,DE是⊙O的切线(1分)
证明:连接OD
∵AB是⊙O的直径
∴AO=OB
∵点D是BC的中点
∴BD=DC,
∴OD是△ACB的中位线,
∴OD∥AC (2分)
∴DE⊥OD
即DE是⊙O的切线(3分)
(2)①∵AC为⊙O的切线
∴AC⊥AB
∵DE∥AB
∴DE⊥AC
∵点E是AC中点
∴点D是BC中点(4分)
∴OD⊥DE (5分)
∵AO=OD
∴四边形AODE是正方形(6分)
∵AB=2
∴AD=
∴ =
= =
= =2
=2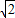 -2 (8分)
-2 (8分)
②由图形可知,S阴影=S正方形AODC-S扇形OAD∵S正方形=1×1=1平方单位(9分)
∵S扇形= =
= 平方单位(10分)
平方单位(10分)
∴S阴影=1- 平方单位(11分).
平方单位(11分).
点评:此题综合运用了三角形的中位线定理、切线的判定和性质、正方形的判定和性质以及等腰直角三角形的性质.
(2)①中,连接OD,根据平行线等分线段定理,得到D是BC的中点,根据平行线的性质和切线的性质得到DE⊥AC,结合(1)的结论,则DE也是圆的切线,从而得到OD⊥DE,根据一组邻边相等的矩形是正方形得到正方形AEDO,从而发现等腰直角三角形AOD和ADB,根据AB=2,即可求得AD的长,进一步计算;
②中,阴影部分的面积显然是正方形AEDO的面积减去扇形OAD的面积,根据①中的结论即可计算.
解答:
 解:(1)如图所示,
解:(1)如图所示,当DE⊥AC时,DE是⊙O的切线(1分)
证明:连接OD
∵AB是⊙O的直径
∴AO=OB
∵点D是BC的中点
∴BD=DC,
∴OD是△ACB的中位线,
∴OD∥AC (2分)
∴DE⊥OD
即DE是⊙O的切线(3分)
(2)①∵AC为⊙O的切线
∴AC⊥AB
∵DE∥AB
∴DE⊥AC
∵点E是AC中点
∴点D是BC中点(4分)
∴OD⊥DE (5分)
∵AO=OD
∴四边形AODE是正方形(6分)
∵AB=2
∴AD=

∴
 =
= =
= =2
=2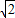 -2 (8分)
-2 (8分)②由图形可知,S阴影=S正方形AODC-S扇形OAD∵S正方形=1×1=1平方单位(9分)
∵S扇形=
 =
= 平方单位(10分)
平方单位(10分)∴S阴影=1-
 平方单位(11分).
平方单位(11分).点评:此题综合运用了三角形的中位线定理、切线的判定和性质、正方形的判定和性质以及等腰直角三角形的性质.

练习册系列答案
相关题目


 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由.