题目内容
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=3,BC=5,E是边CD的中点,连结BE并延长与AD的延长线相交于点F. 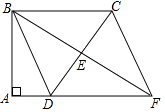
(1)求证:四边形BDFC是平行四边形.
(2)若BD=BC,求四边形BDFC的面积.
【答案】
(1)证明:∵∠A=∠ABC=90°,
∴BC∥AD,
∴∠CBE=∠DFE,
又∵E是边CD的中点,
∴CE=DE,
在△BEC与△FED中, 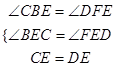 ,
,
∴△BEC≌△FED,
∴BE=FE
∴四边形BDFC是平行四边形;
(2)解:∵BD=BC=5,
∴AB= ![]() =
= ![]() =4,
=4,
∴四边形BDFC的面积=BCAB=5×4=20.
【解析】(1)根据同旁内角互补两直线平行求出BC∥AD,再根据两直线平行,内错角相等可得∠CBE=∠DFE,然后利用“角角边”证明△BEC和△FCD全等,根据全等三角形对应边相等可得BE=EF,然后利用对角线互相平分的四边形是平行四边形证明即可;(2)利用勾股定理列式求出AB,然后利用平行四边形的面积公式列式计算即可得.
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.

练习册系列答案
相关题目
【题目】某“优质花海专用花籽”的价格为60元/kg,如果一次性购买5kg以上的花籽,超过5kg的部分的花籽的价格打8折.
(1)根据题意,填写下表:
购买花籽的重量/kg | 3 | 4 | 5 | 6 | … |
付款金额/元 | 180 | 300 |
(2)设购买花籽的重量为xkg,付款金额为y元,求y关于x的函数解析式;
(3)若花海园丁李伯伯一次购买该花籽花费了540元,求他购买花籽的重量.