Question

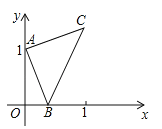
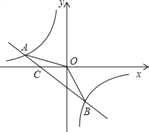
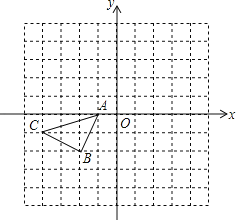
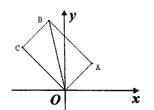
【题目】将－矩形OABC置于直角坐标系中，若∠ABO=30°，A（3，4），则点C的坐标为_____．

Answer 1

【答案】（，）

【解析】

如图，过点A作AD⊥x轴，过点C作CE⊥x轴，垂足分别为D、E，先求出OA长，再根据矩形的性质得到∠COA=∠OAB=90°，OC=AB，由∠ABO=30°，利用三角函数求出AB的长，证明△COE∽△OAD，继而根据相似三角形对应边成比例求出OE=4，CE=3，再根据点C在第二象限即可求得答案.

如图，过点A作AD⊥x轴，过点C作CE⊥x轴，垂足分别为D、E，

则∠ADO=∠CEO=90°，

∵A(3，4)，∴OD=3，AD=4，

∴OA==5，

∵四边形OABC是矩形，

∴∠COA=∠OAB=90°，OC=AB，

∵∠ABO=30°，

∴AB=，∴OC=5，

∵∠COE+∠COA+∠AOD=180°，∠OAD+∠AOD=90°，

∴∠COE=∠OAD，

又∠ADO=∠CEO=90°，

∴△COE∽△OAD，

∴，

即，

∴OE=4，CE=3，

∵点C在第二象限，

∴点C坐标为(，)，

故答案为：(，).