题目内容
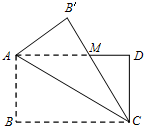 如图,将长方形纸片ABCD沿对角线AC折叠,使点B落在点B′处,CB′交AD于点M.试说明△AMC的形状,并说明理由.
如图,将长方形纸片ABCD沿对角线AC折叠,使点B落在点B′处,CB′交AD于点M.试说明△AMC的形状,并说明理由.分析:由将长方形纸片ABCD沿对角线AC折叠,根据长方形的性质与折叠的性质,易得∠MAC=∠ACM=∠ACB,继而可证得△AMC是等腰三角形.
解答:解:△AMC是等腰三角形.
理由:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠MAC=∠ACB,
由折叠的性质可得:∠ACB=∠ACM,
∴∠MAC=∠ACM,
∴AM=CM,
即△AMC是等腰三角形.
理由:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠MAC=∠ACB,
由折叠的性质可得:∠ACB=∠ACM,
∴∠MAC=∠ACM,
∴AM=CM,
即△AMC是等腰三角形.
点评:此题考查了等腰三角形的判定以及折叠的性质.此题难度不大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
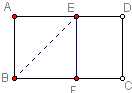 15、如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
15、如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( ) 19、如图,将长方形纸片的一角折叠,使顶点A落在A′处,EF为折痕,再将另一角折叠,使顶点B落在EA′上的B′点处,折痕为EG,则∠FEG等于
19、如图,将长方形纸片的一角折叠,使顶点A落在A′处,EF为折痕,再将另一角折叠,使顶点B落在EA′上的B′点处,折痕为EG,则∠FEG等于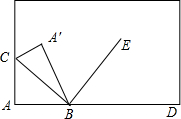 如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的角平分线,求∠CBE的度数,并说明理由.
如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的角平分线,求∠CBE的度数,并说明理由.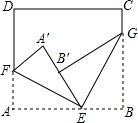 如图,将长方形纸片的一角斜折,使顶点A落在A′处,EF为折痕;再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EG;观察并估计∠FEG=
如图,将长方形纸片的一角斜折,使顶点A落在A′处,EF为折痕;再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EG;观察并估计∠FEG=