题目内容
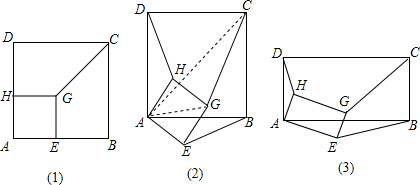
(2012•资阳)(1)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果(不必写计算过程);
(2)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD:GC:EB;
(3)把图(2)中的正方形都换成矩形,如图(3),且已知DA:AB=HA:AE=m:n,此时HD:GC:EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).
(2)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD:GC:EB;
(3)把图(2)中的正方形都换成矩形,如图(3),且已知DA:AB=HA:AE=m:n,此时HD:GC:EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).

分析:(1)首先连接AG,由正方形AEGH的顶点E、H在正方形ABCD的边上,易证得∠GAE=∠CAB=45°,AE=AH,AB=AD,即A,G,C共线,继而可得HD=BE,GC=
BE,即可求得HD:GC:EB的值;
(2)连接AG、AC,由△ADC和△AHG都是等腰直角三角形,易证得△DAH∽△CAG与△DAH≌△BAE,利用相似三角形的对应边成比例与正方形的性质,即可求得HD:GC:EB的值;
(3)由DA:AB=HA:AE=m:n,易证得△ADC∽△AHG,△DAH∽△CAG,△ADH∽△ABE,利用相似三角形的对应边成比例与勾股定理即可求得HD:GC:EB的值.
| 2 |
(2)连接AG、AC,由△ADC和△AHG都是等腰直角三角形,易证得△DAH∽△CAG与△DAH≌△BAE,利用相似三角形的对应边成比例与正方形的性质,即可求得HD:GC:EB的值;
(3)由DA:AB=HA:AE=m:n,易证得△ADC∽△AHG,△DAH∽△CAG,△ADH∽△ABE,利用相似三角形的对应边成比例与勾股定理即可求得HD:GC:EB的值.
解答:解:(1)连接AG,
∵正方形AEGH的顶点E、H在正方形ABCD的边上,
∴∠GAE=∠CAB=45°,AE=AH,AB=AD,
∴A,G,C共线,AB-AE=AD-AH,
∴HD=BE,
∵AG=
=
AE,AC=
=
AB,
∴GC=AC-AG=
AB-
AE=
(AB-AE)=
BE,
∴HD:GC:EB=1:
:1;
(2)连接AG、AC,
∵△ADC和△AHG都是等腰直角三角形,
∴AD:AC=AH:AG=1:
,∠DAC=∠HAG=45°,
∴∠DAH=∠CAG,
∴△DAH∽△CAG,
∴HD:GC=AD:AC=1:
,
∵∠DAB=∠HAE=90°,
∴∠DAH=∠BAE,
在△DAH和△BAE中,
,
∴△DAH≌△BAE(SAS),
∴HD=EB,
∴HD:GC:EB=1:
:1;
(3)有变化,
连接AG、AC,DA:AB=HA:AE=m:n,
∵∠ADC=∠AHG=90°,
∴△ADC∽△AHG,
∴AD:AC=AH:AG=m:
,∠DAC=∠HAG,
∴∠DAH=∠CAG,
∴△DAH∽△CAG,
∴HD:GC=AD:AC=m:
,
∵∠DAB=∠HAE=90°,
∴∠DAH=∠BAE,
∵DA:AB=HA:AE=m:n,
∴△ADH∽△ABE,
∴DH:BE=AD:AB=m:n,
∴HD:GC:EB=m:
:n.
∵正方形AEGH的顶点E、H在正方形ABCD的边上,
∴∠GAE=∠CAB=45°,AE=AH,AB=AD,

∴A,G,C共线,AB-AE=AD-AH,
∴HD=BE,
∵AG=
| AE |
| sin45° |
| 2 |
| AB |
| sin45° |
| 2 |
∴GC=AC-AG=
| 2 |
| 2 |
| 2 |
| 2 |
∴HD:GC:EB=1:
| 2 |
(2)连接AG、AC,
∵△ADC和△AHG都是等腰直角三角形,
∴AD:AC=AH:AG=1:
| 2 |
∴∠DAH=∠CAG,
∴△DAH∽△CAG,
∴HD:GC=AD:AC=1:
| 2 |
∵∠DAB=∠HAE=90°,
∴∠DAH=∠BAE,
在△DAH和△BAE中,
|
∴△DAH≌△BAE(SAS),
∴HD=EB,
∴HD:GC:EB=1:
| 2 |
(3)有变化,
连接AG、AC,DA:AB=HA:AE=m:n,
∵∠ADC=∠AHG=90°,
∴△ADC∽△AHG,
∴AD:AC=AH:AG=m:
| m2+n2 |
∴∠DAH=∠CAG,
∴△DAH∽△CAG,
∴HD:GC=AD:AC=m:
| m2+n2 |
∵∠DAB=∠HAE=90°,
∴∠DAH=∠BAE,
∵DA:AB=HA:AE=m:n,
∴△ADH∽△ABE,
∴DH:BE=AD:AB=m:n,
∴HD:GC:EB=m:
| m2+n2 |
点评:此题考查了相似三角形的判定与性质、正方形的性质、矩形的性质、全等三角形的判定与性质以及勾股定理等知识.此题综合性较强,难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 (2012•资阳)如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
(2012•资阳)如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )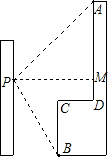 (2012•资阳)小强在教学楼的点P处观察对面的办公大楼.为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米.求点P到AD的距离(用含根号的式子表示).
(2012•资阳)小强在教学楼的点P处观察对面的办公大楼.为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米.求点P到AD的距离(用含根号的式子表示). (2012•资阳)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接EP、CP、OP.
(2012•资阳)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接EP、CP、OP.