Question

【题目】如图，D为⊙O上一点，点C在直径BA的延长线上，∠CDA=∠CBD．

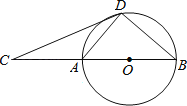
（1）求证：CD是⊙O的切线；

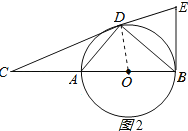
（2）过点B作⊙O的切线交CD的延长线于点E，若AB=6，tan∠CDA=，依题意补全图形并求DE的长．

Answer 1

【答案】（1）见解析；（2）．

【解析】

试题分析：（1）连OD，OE，根据圆周角定理得到∠ADO+∠1=90°，而∠CDA=∠CBD，∠CBD=∠1，于是∠CDA+∠ADO=90°；

（2）根据切线的性质得到ED=EB，OE⊥BD，则∠ABD=∠OEB，得到tan∠CDA=tan∠OEB==，易证Rt△CDO∽Rt△CBE，得到=，

求得CD，然后在Rt△CBE中，运用勾股定理可计算出BE的长，由切线长定理即可得DE的长．

（1）证明：连OD，OE，如图1所示，

∵AB为直径，

∴∠ADB=90°，

即∠ADO+∠BDO=90°，

又∵∠CDA=∠CBD，

而∠CBD=∠BDO，

∴∠BDO=∠CDA，

∴∠CDA+∠ADO=90°，

即∠CDO=90°，

∴CD⊥OD，

∴CD是⊙O的切线；

（2）解：如图2所示：

∵EB为⊙O的切线，

∴ED=EB，OE⊥DB，

∴∠ABD+∠DBE=90°，∠OEB+∠DBE=90°，

∴∠ABD=∠OEB，

∴∠CDA=∠OEB．

而tan∠CDA=，

∴tan∠OEB==，

∵Rt△CDO∽Rt△CBE，

∴=，

∴CD=×6=4，

在Rt△CBE中，设BE=x，

∴（x+4）2=x2+62，

解得：x=．

即BE的长为，

∴DE=BE=．