题目内容
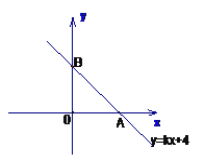
【题目】如图，在直角坐标系中，直线y=kx+4与x 轴正半轴交于一点A，与y轴交于点B，已知△OAB的面积为10，求这条直线的解析式。
【答案】
【解析】试题分析: 先根据坐标轴上点的坐标特征得到A（4k，0），B（0，4），再根据三角形面积公式得到
（
）4＝10，然后解方程求出k的值即可得到直线解析式．
试题解析:
当y＝0时，kx＋4＝0，解得x＝
，则A（
，0），
当x＝0时，y＝kx＋4＝4，则B（0，4），
因为△OAB的面积为10，
所以
（
）4＝10，解得k＝
，
所以直线解析式为y＝
x＋4．
点睛: 本题考查了待定系数法求一次函数解析式：先设出函数的一般形式，如求一次函数的解析式时，先设y＝kx＋b；将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；解方程或方程组，求出待定系数的值，进而写出函数解析式．
练习册系列答案
相关题目
