题目内容
等腰梯形的腰长为5cm，上、下底的长分别为6cm和12cm，则它的面积为分析：过A作AE⊥BC，根据已知可求得BE的长，再根据勾股定理求得AE的长，从而利用梯形的面积公式求解即可．
解答：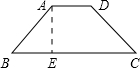
解：由题意得：BE=
（BC-AD）=3，
∴AE=
=4，
∴梯形的面积=
（AD+BC）×AE=36cm2．
故答案为：36cm2．
解：由题意得：BE=| 1 |
| 2 |
∴AE=
| AB2-BE2 |
∴梯形的面积=
| 1 |
| 2 |
故答案为：36cm2．
点评：本题主要考查勾股定理及等腰梯形的性质，难度不大，解出梯形的高是关键．
练习册系列答案
相关题目
已知等腰梯形的底角为45°，梯形的高等于上底，且下底的长为9，那么梯形的腰长为（ ）
| A、3 | ||
| B、5 | ||
C、3
| ||
D、2
|
等腰梯形的上底长为2，下底长为10，高为3，则它的腰长为（ ）
| A、4 | B、5 | C、7 | D、10 |
等腰梯形的一底角为60°，两底之和为11，下底比上底的2倍多2．则腰长为（ ）
| A、3 | B、5 | C、8 | D、9 |
