Question

等腰梯形的一底角为60°，两底之和为11，下底比上底的2倍多2．则腰长为（　　）

• A、3
• B、5
• C、8
• D、9

Answer 1

分析：根据题意画出示意图，然后可求出BE的长度，进而结合三角函数值可求出腰长．

解答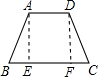：解：所画示意图如上：
∵两底之和为11，下底比上底的2倍多2，
∴可得AD=3，BC=8，
又∵ABCD是等腰梯形，
∴可得BE=CF=

1

2

（BC-AD）=

5

2

，
∴AB=

BE

cos∠B

=5．
故选B．

点评：本题考查等腰梯形的性质，比较简单，解答本题时注意先画出示意图，这样对于分析会带来很大的方便．