Question

【题目】如图，矩形ABCD中，点P是线段AD上一动点，O为BD的中点，PO的延长线交BC于Q．
（1）求证：OP=OQ；
（2）若AD=8厘米，AB=6厘米，P从点A出发，以1厘米/秒的速度向D运动（不与D重合）．设点P运动时间为t秒，请用t表示PD的长；并求t为何值时，四边形PBQD是菱形．

Answer 1

【答案】
（1）证明：∵四边形ABCD是矩形，

∴AD∥BC，

∴∠PDO=∠QBO，

又∵O为BD的中点，

∴OB=OD，

在△POD与△QOB中，

∵

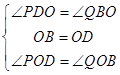
∴△POD≌△QOB（ASA），

∴OP=OQ；

（2）解：PD=8﹣t，

∵四边形PBQD是菱形，

∴PD=BP=8﹣t，

∵四边形ABCD是矩形，

∴∠A=90°，

在Rt△ABP中，由勾股定理得：AB2+AP2=BP2，

即62+t2=（8﹣t）2，

解得：t= ，

即运动时间为 秒时，四边形PBQD是菱形．

【解析】（1）本题需先根据四边形ABCD是矩形，得出AD∥BC，∠PDO=∠QBO，再根据O为BD的中点得出△POD≌△QOB，即可证出OP=OQ．（2）本题需先根据已知条件得出∠A的度数，再根据AD=8厘米，AB=6厘米，得出BD和OD的长，再根据四边形PBQD是菱形时，即可求出t的值，判断出四边形PBQD是菱形．
【考点精析】关于本题考查的勾股定理的概念和菱形的性质，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能得出正确答案．