题目内容
（2009•莱芜）如图，在四边形ABCD中，已知AB与CD不平行，∠ABD=∠ACD，请你添加一个条件： ，使得加上这个条件后能够推出AD∥BC且AB=CD．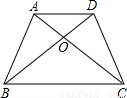
【答案】分析：先证四边形AECO是梯形，再说明是等腰梯形．由题意可知，∠ABD=∠ACD，AD是△BAD和△CDA的公共边，则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA，同理可添加∠DBC=∠ACB，∠ABC=∠DCB，OB=OC，OA=OD，从而推出AD∥BC且AB=CD．
解答：解：由题意可知，∠ABD=∠ACD，AD是△BAD和△CDA的公共边，
则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA
∴△BAD≌△CDA
∴BD=AC，AB=DC，
∵∠DAC=∠ADB，
∴OA=OD，
∴OB=OC，
∴∠OBC=∠OCB，
∵∠AOD=∠BOC，
∴∠DAC=∠ACB=∠ADB=∠DBC，
∴AD∥BC
同理可添加∠DBC=∠ACB，∠ABC=∠DCB，OB=OC，OA=OD，从而推出AD∥BC且AB=CD．
本题答案不唯一，如∠DAC=∠ADB，∠BAD=∠CDA，∠DBC=∠ACB，∠ABC=∠DCB，OB=OC，OA=OD．（任选其一）
点评：这是一道考查等腰梯形的判定方法的开放性的题，答案不唯一．
解答：解：由题意可知，∠ABD=∠ACD，AD是△BAD和△CDA的公共边，
则可以再添加一组角∠DAC=∠ADB或∠BAD=∠CDA
∴△BAD≌△CDA
∴BD=AC，AB=DC，
∵∠DAC=∠ADB，
∴OA=OD，
∴OB=OC，
∴∠OBC=∠OCB，
∵∠AOD=∠BOC，
∴∠DAC=∠ACB=∠ADB=∠DBC，
∴AD∥BC
同理可添加∠DBC=∠ACB，∠ABC=∠DCB，OB=OC，OA=OD，从而推出AD∥BC且AB=CD．
本题答案不唯一，如∠DAC=∠ADB，∠BAD=∠CDA，∠DBC=∠ACB，∠ABC=∠DCB，OB=OC，OA=OD．（任选其一）
点评：这是一道考查等腰梯形的判定方法的开放性的题，答案不唯一．
练习册系列答案
名校课堂系列答案
相关题目
（2009•莱芜）如图，⊙O的直径AB=4，C为圆周上一点，AC=2，过点C作⊙O的切线l，过点B作l的垂线BD，垂足为D，BD与⊙O交于点E．
（2009•莱芜）如图，两个同心圆的圆心为O，EC是大圆的一条弦，交小圆于D、B两点，已知弦心距OA=3，DB=8，EC=l2，则圆环（阴影部分）的面积为（ ）
