题目内容
【题目】△ABC是一块锐角三角形余料,边BC=180mm,高AD=120mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.
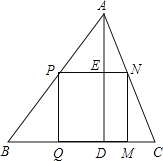
(1)若这个矩形是正方形,那么边长是多少?
(2)若这个矩形的长是宽的2倍,则边长是多少?
【答案】(1)72mm.(2)矩形的长为90mm,宽是45mm或者长为![]() mm,宽为
mm,宽为![]() mm.
mm.
【解析】
试题分析:(1)设出边长为xmm,由正方形的性质得出PN∥BC,PQ∥AD,根据平行线的性质,可以得出比例关系式,![]() =
=![]() 、
、![]() =
=![]() ,代入数据求解即可.
,代入数据求解即可.
(2)设宽为xmm,则长为2xmm,同(1)列出比例关系求解,但是要注意有两种情况,PQ可以为长也可以为宽,分两种情况分别求解即可.
解:(1)设边长为xmm,
∵矩形为正方形,
∴PN∥BC,PQ∥AD,
根据平行线的性质可以得出:![]() =
=![]() 、
、![]() =
=![]() ,
,
由题意知PQ=x,BC=180mm,AD=120mm,PN=x,
即![]() =
=![]() ,
,![]() =
=![]() ,
,
∵AP+BP=AB,
∴![]() +
+![]() =
=![]() +
+![]() =1,
=1,
解得x=72.
答:若这个矩形是正方形,那么边长是72mm.
(2)设边宽为xmm,则长为2xmm,
∵四边形PNMQ为矩形,
∴PN∥BC,PQ∥AD,
根据平行线的性质可以得出:![]() =
=![]() 、
、![]() =
=![]() ,
,
①PQ为长,PN为宽:
由题意知PQ=2xmm,AD=120mm,BC=180mm,AN=xmm,
即![]() =
=![]() ,
,![]() =
=![]() ,
,
∵AP+BP=AB,
∴![]() +
+![]() =
=![]() +
+![]() =1,
=1,
解得x=45,2x=90.
即长为90mm,宽为45mm.
②PQ为宽,PN为长:
由题意知PQ=xmm,AD=120mm,BC=180mm,PN=2xmm,
即![]() =
=![]() ,
,![]() =
=![]() ,
,
∵AP+BP=AB,
∴![]() +
+![]() =
=![]() +
+![]() =1,
=1,
解得x=![]() ,2x=
,2x=![]() .
.
即长为![]() mm,宽为
mm,宽为![]() mm.
mm.
答:矩形的长为90mm,宽是45mm或者长为![]() mm,宽为
mm,宽为![]() mm.
mm.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广节能灯,为响应号召,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?

