题目内容
设C为线段AB的中点,四边形BCDE是以BC为一边的正方形.以B为圆心,BD长为半径的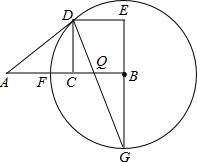 ⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
求证:(1)AD是⊙B的切线;
(2)AD=AQ;
(3)BC2=CF•EG.
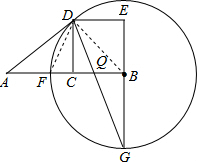 证明:(1)连接BD,
证明:(1)连接BD,∵四边形BCDE是正方形,
∴∠DBA=45°,∠DCB=90°,即DC⊥AB,
∵C为AB的中点,
∴CD是线段AB的垂直平分线,
∴AD=BD,
∴∠DAB=∠DBA=45°,
∴∠ADB=90°,
即BD⊥AD,
∵BD为半径,
∴AD是⊙B的切线;
(2)∵BD=BG,
∴∠BDG=∠G,
∵CD∥BE,
∴∠CDG=∠G,
∴∠G=∠CDG=∠BDG=
 ∠BCD=22.5°,
∠BCD=22.5°,∴∠ADQ=90°-∠BDG=67.5°,∠AQB=∠BQG=90°-∠G=67.5°,
∴∠ADQ=∠AQD,
∴AD=AQ;
(3)连接DF,
在△BDF中,BD=BF,
∴∠BFD=∠BDF,
又∵∠DBF=45°,
∴∠BFD=∠BDF=67.5°,
∵∠GDB=22.5°,
在Rt△DEF与Rt△GCD中,
∵∠GDE=∠GDB+∠BDE=67.5°=∠DFE,∠DCF=∠E=90°,
∴Rt△DCF∽Rt△GED,
∴
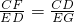 ,
,又∵CD=DE=BC,
∴BC2=CF•EG.
分析:(1)连接BD,由DC⊥AB,C为AB的中点,由线段垂直平分线的性质,可得AD=BD,再根据正方形的性质,可得∠ADB=90°;
(2)由BD=BG与CD∥BE,利用等边对等角与平行线的性质,即可求得∠G=∠CDG=∠BDG=
 ∠BCD=22.5°,继而求得∠ADQ=∠AQD=67.5°,由等角对等边,可证得AD=AQ;
∠BCD=22.5°,继而求得∠ADQ=∠AQD=67.5°,由等角对等边,可证得AD=AQ;(3)易求得∠GDE=∠GDB+∠BDE=67.5°=∠DFE,∠DCF=∠E=90°,即可证得Rt△DCF∽Rt△GED,根据相似三角形的对应边成比例,即可证得结论.
点评:此题考查了相似三角形的判定与性质、切线的判定与性质、正方形的性质以及等腰三角形的判定与性质.此题综合性较强,难度较大,注意掌握数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
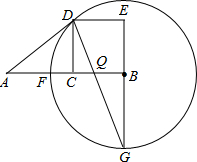 ⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
 x+2与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
x+2与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点. 的图象过点D,求k值;
的图象过点D,求k值; 个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
