题目内容
观察下列各式及其变形过程:2
|
|
|
2+
|
(1)按上述等式及其验证过程的基本思路,猜想3
|
(2)针对上述各式反映的规律,写出用n(n为自然数,n≥2)表示的算式,并证明;
(3)依上面规律,写出用n表示下列各式的规律:2
|
2-
|
|
3-
|
分析:(1)由题中的变形过程规律可以容易得出3
的变形过程;
(2)由此规律可以推广到当n≥2时的变形过程;
(3)从2
=
,3
=
和题干的变形形式可以得出它的变形规律.
|
(2)由此规律可以推广到当n≥2时的变形过程;
(3)从2
|
2-
|
|
3-
|
解答:解:(1)从题目的变形可以得出3
=
=
=
.
证明:
=
=
=
=3
.所以变形正确.
(2)从上面两个变形可以看出3=22-1,8=32-1,
所以当为n时,分母为n2-1;
故当n≥2时,可以表示为n
=
;
证明:n
=
=
=
.
(3)有5=22+1,10=32+1;故当为n时有
n
=
|
|
|
3+
|
证明:
3+
|
|
|
|
|
(2)从上面两个变形可以看出3=22-1,8=32-1,
所以当为n时,分母为n2-1;
故当n≥2时,可以表示为n
|
n+
|
证明:n
|
|
|
n+
|
(3)有5=22+1,10=32+1;故当为n时有
n
|
n-
|
点评:本题考查同学们对于题目中所给出的已知条件得出其中的规律的问题,需要学生有一定的数学思想.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
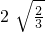 =
= =
=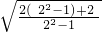 =
=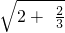
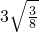 的变形结果并进行证明;
的变形结果并进行证明;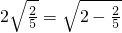 ,
,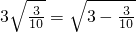 ,…(不要求证明).
,…(不要求证明).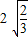 =
=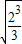 =
=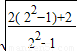 =
=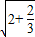
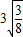 的变形结果并进行证明;
的变形结果并进行证明;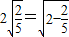 ,
,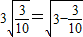 ,…(不要求证明).
,…(不要求证明).