题目内容
(2005•枣庄)如图,在矩形ABCD中,AB=5,BC=12,⊙O1和⊙O2分别是△ABC和△ADC的内切圆,则O1O2= .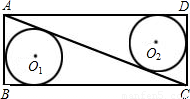
【答案】分析:本题的解题思想是通过构造一直角三角形,把线段O1O2放到一直角三角形中,再利用勾股定理就可解得.
解答: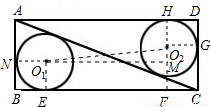 解:∵矩形ABCD中,AB=5,BC=12;
解:∵矩形ABCD中,AB=5,BC=12;
∴AC=13,△ABC≌△CDA,则⊙O1和⊙O2的半径相等.
如图,过O1作AB、BC的垂线分别交AB、BC于N、E,过O2作BC、CD、AD的垂线分别交BC、CD、AD于F、G、H;
∵∠B=90°,
∴四边形O1NBE是正方形;
设圆的半径为r,根据切线长定理5-r+12-r=13,解得r=2,
∴BE=BN=2,
同理DG=HD=CF=2,
∴CG=FO2=3,EF=12-4=8;
过O1作O1M⊥FO2于M,则O1M=EF=8,FM=BN=2,
∴O2M=1,
在Rt△O1O2M中,O1O2=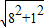 =
=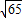 .
.
点评:本题主要考查了三角形的内切圆的性质及切线长定理,作辅助线是解题的关键.
解答:
 解:∵矩形ABCD中,AB=5,BC=12;
解:∵矩形ABCD中,AB=5,BC=12;∴AC=13,△ABC≌△CDA,则⊙O1和⊙O2的半径相等.
如图,过O1作AB、BC的垂线分别交AB、BC于N、E,过O2作BC、CD、AD的垂线分别交BC、CD、AD于F、G、H;
∵∠B=90°,
∴四边形O1NBE是正方形;
设圆的半径为r,根据切线长定理5-r+12-r=13,解得r=2,
∴BE=BN=2,
同理DG=HD=CF=2,
∴CG=FO2=3,EF=12-4=8;
过O1作O1M⊥FO2于M,则O1M=EF=8,FM=BN=2,
∴O2M=1,
在Rt△O1O2M中,O1O2=
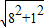 =
=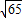 .
.点评:本题主要考查了三角形的内切圆的性质及切线长定理,作辅助线是解题的关键.

练习册系列答案
相关题目



