题目内容
【题目】如图，以圆O为圆心，半径为1的弧交坐标轴于A，B两点，P是 
上一点（不与A，B重合），连接OP，设∠POB=α，则点P的坐标是（ ）
A.（sinα，sinα）
B.（cosα，cosα）
C.（cosα，sinα）
D.（sinα，cosα）
【答案】C
【解析】解：过P作PQ⊥OB，交OB于点Q，
在Rt△OPQ中，OP=1，∠POQ=α，
∴sinα= 
，cosα= 
，即PQ=sinα，OQ=cosα，
则P的坐标为（cosα，sinα），
故选C．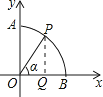
过P作PQ⊥OB，交OB于点Q，在直角三角形OPQ中，利用锐角三角函数定义表示出OQ与PQ，即可确定出P的坐标．此题考查了解直角三角形，以及坐标与图形性质，熟练掌握锐角三角函数定义是解本题的关键．
练习册系列答案
53随堂测系列答案
相关题目
【题目】某校一间阶梯教室中，第1排的座位数为a，从第2排开始，每一排都比前一排增加两个座位．
（1）请你在下表的空格里填写一个适当的式子：
第1排的 座位数 | 第2排的 座位数 | 第3排的 座位数 | 第4排的 座位数 | … |
a | a+2 | a+4 | … |
（2）写出第n排座位数的表达式；
（3）求当a＝20时，第10排的座位数是多少？若这间阶梯教室共有15排，那么最多可容纳多少学员？
