题目内容
【题目】已知y=y1+y2, y1与![]() 成正比例,y2与x2成反比例.当x=1时,y=-12;
成正比例,y2与x2成反比例.当x=1时,y=-12;
当x=4时,y=7.(1)求y与x的函数关系式和x的取值范围;(2)当x=![]() 时,求y的值.
时,求y的值.
【答案】![]() ;(2)
;(2)![]() ;
;
【解析】试题分析:根据题意可设y1=k1![]() ,y2=
,y2=![]() ,所以y=k1
,所以y=k1![]() +
+![]() ;又因为当x=1时,y=-12;当x=4时,y=7,所以将点代入解析式即可得到方程组,解方程即可求得y与x的函数关系式.根据已知可得x>0.将x=
;又因为当x=1时,y=-12;当x=4时,y=7,所以将点代入解析式即可得到方程组,解方程即可求得y与x的函数关系式.根据已知可得x>0.将x=![]() 代入函数解析式,即可求得y的值.
代入函数解析式,即可求得y的值.
试题解析:(1)设y1=k1![]() ,y2=
,y2=![]() ,所以y=k1
,所以y=k1![]() +
+![]() ;
;
∵当x=1时,y=-12;当x=4时,y=7.
∴ .
.
解得: ![]() .
.
∴y与x的函数关系式为y=4![]() -
-![]() ,
,
∵x≥0,x2≠0,
∴x的取范围为x>0;
(2)当x=![]() 时,
时,
y=4×![]() -
-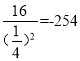 .
.
∴y的值为-254.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
