题目内容
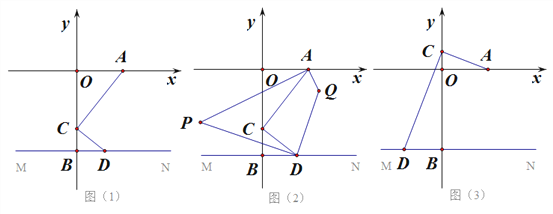
【题目】如图,在平面直角坐标系中,点A在X轴正半轴上,B在Y轴的负半轴,过点B画MN∥x轴;C是Y轴上一点,连接AC,作CD⊥CA.
(1)如图(1),请直接写出∠CA0与∠CDB的数量关系.
(2)如图(2),在题(1)的条件下,∠CAO的角平分线与∠CDB的角平分线相交于点P,求∠APD的度数.
(3)如图(2),在题(1)、(2)的条件下,∠CAX的角平分线与∠CDN的角平分线相交于点Q,请直接写出∠APD与∠AQD数量关系.
(4)如图(3),点C在Y轴的正半轴上运动时,∠CAO的角平分线所在的直线与∠CDB的角平分线相交于点P,∠APD的大小是否变化?若不变,直接写出其值;若变化,说明理由.
【答案】(1)∠CAO+∠CDB=90;
(2)∠APD=45;
(3)∠APD+∠AQD=180;
(4)∠APD的大小不变,为45.
【解析】试题分析:(1)根据平行线的性质可直接写出结果;
(2)根据(1)的结论,由角平分线的性质可直接求解;
(3)根据(1)(2)的结论,由角平分线的性质可直写出结果;
(4)同上面的解题方法,直接判断即可.
试题解析:(1)∠CA0+∠CDB=90
(2)∠APD=45
(3)∠APD+∠AQD=180
(4)∠APD的大小不变,为45

练习册系列答案
相关题目