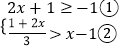题目内容
【题目】据我国古代《周髀算经》记载,大约公元1120年,商高曾对周公说过一段话,其意思是将一根直尺折成一个直角,两端连接得一个直角三角形,如果勾是三,股是四,那么弦就等于五,后人概括为“勾三股四弦五”。
(1)观察:3,4,5; 5,12,13; 7,24,25……发现这些勾股数的勾都是奇数,且从3起就没有间断过。计算![]() ,
, ![]() 与
与![]() ,
, ![]() 并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;
并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;
(2)根据(1)的规律,用n(n为奇数且n≥3)的代数式来表示所有这些勾股数的勾、股、弦,合理猜想它们之间的两种相等关系并对其一种猜想加以说明。
【答案】(1)![]() ,
, ![]() ;(2)勾、股、弦的算式为n,
;(2)勾、股、弦的算式为n, ![]() ,
, ![]()
两种相等关系为: ![]() ,
, ![]()
理由见解析
【解析】试题分析:(1)根据所提供的例子发现股是勾的平方减去1的二分之一,弦是勾的平方加1的二分之一;
(2)①:弦股=1;关系式②:勾2+股2=弦2.
试题解析:(1)∵![]()
∴7,24,25的股的算式为![]()
弦的算式为![]()
(2)当n为奇数且![]() ,勾、股、弦的代数式分别为:
,勾、股、弦的代数式分别为: ![]()
例如关系式①:弦股=1;关系式②:勾2+股2=弦2.
证明关系式①:弦股![]()
或证明关系式②:勾2+股2![]() =弦2.
=弦2.
∴猜想得证;

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目