Question

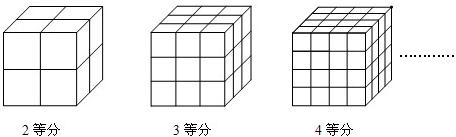
将一个正方体的表面涂上颜色．如图把正方体的棱2等分，然后沿等分线把正方体切开，能够得到8个小正方体，通过观察我们可以发现8个小正方体全是3个面涂有颜色的．
如果把正方体的棱三等分，然后沿等分线把正方体切开，能够得到27个小正方体，通过观察我们可以发现这些小正方体中有8个是3个面涂有颜色的，有12个是2个面涂有颜色的，有6个是1个面涂有颜色的，还有1个各个面都没有涂色．

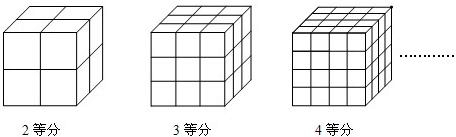
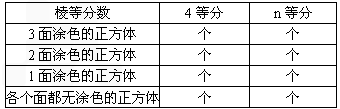
（1）如果把正方体的棱4等分，所得小正方体表面涂色情况如何呢？把正方体的棱n等分呢？（请填写下表）：

棱等分数	4等分	n等分
3面涂色的正方体	个	个
2面涂色的正方体	个	个
1面涂色的正方体	个	个
各个面都无涂色的正方体	个	个

（2）请直接写出将棱7等分时只有一个面涂色的小正方体的个数．

Answer 1

解：（1）三面涂色8，8；
二面涂色24，12（n-2），
一面涂色24，6（n-2）²
各面均不涂色8，（n-2）³；

（2）当n=7时，
6（n-2）²
=6×（7-2）²
=150，
所以一面涂色的小正方体有150个．
分析：（1）根据长方体的分割规律可分别得到4等分时的所得小正方体表面涂色情况，由特殊推广到一般即可得到n等分时所得小正方体表面涂色情况；
（2）直接把n=7代入（1）中所得的规律中即可．
点评：主要考查了立体图形的认识和用特殊归纳一般规律的方法．关键是通过正方体的特点来得到有关涂色情况的规律．