题目内容
如图，AC是⊙O的切线，C是切点，线段OA交⊙O于点B，且OB=AB，点P是⊙O上的一个动点，那么∠CAP的最大值是（ ）| A、90° | B、30° | C、120° | D、60° |
练习册系列答案
相关题目
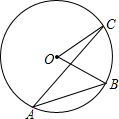如图，在⊙O中，∠BOC=50°，则∠A的度数为（ ）| A、15° | B、25° | C、50° | D、100° |
如图，在平面直角坐标系中，点A、B均在函数y=| k |
| x |
| A、（2，2） | ||
| B、（2，3） | ||
| C、（3，2） | ||
D、（4，
|
如图，PA、PB分别切⊙O于点A、B，若∠P=70°，则∠C的大小为 （ ）| A、40° | B、50° | C、55° | D、60° |
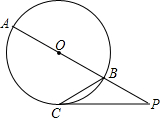如图，AB是⊙O的直径，延长AB至点P，使PB等于半径OB，过点P作⊙O的切线，切点为C，则∠ABC的度数等于（ ）| A、45° | B、50° | C、55° | D、60° |
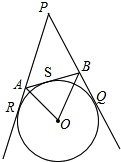如图，PQ、PR、AB是⊙O的切线，切点分别为Q、R、S，若∠APB=40°，则∠A0B等于（ ）| A、40° | B、50° | C、60° | D、70° |
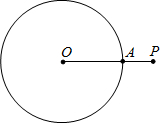如图，P为圆O外一点，OP交圆O于A点，且OA=2AP．甲、乙两人想作一条通过P点且与圆O相切的直线，其作法如下：（甲）以P为圆心，OP长为半径画弧，交圆O于B点，则直线PB即为所求；
（乙）作OP的中垂线，交圆O于B点，则直线PB即为所求．
对于甲、乙两人的作法，下列判断何者正确？（ ）
| A、两人皆正确 | B、两人皆错误 | C、甲正确，乙错误 | D、甲错误，乙正确 |
两圆的半径分别为2cm，3cm，圆心距为2cm，则这两个圆的位置关系是（ ）
| A、外切 | B、相交 | C、内切 | D、内含 |
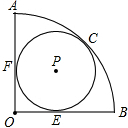如图，扇形OAB，∠AOB=90°，⊙P与OA，OB分别相切于点F，E，并且与弧AB切于点C，则扇形OAB的面积与⊙P的面积比是（ ）A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|