题目内容
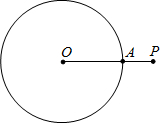如图，P为圆O外一点，OP交圆O于A点，且OA=2AP．甲、乙两人想作一条通过P点且与圆O相切的直线，其作法如下：（甲）以P为圆心，OP长为半径画弧，交圆O于B点，则直线PB即为所求；
（乙）作OP的中垂线，交圆O于B点，则直线PB即为所求．
对于甲、乙两人的作法，下列判断何者正确？（ ）
| A、两人皆正确 | B、两人皆错误 | C、甲正确，乙错误 | D、甲错误，乙正确 |
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
如图，已知⊙O中∠AOB度数为100°，C是圆周上的一点，则∠ACB的度数为（ ）| A、130° | B、100° | C、80° | D、50° |
如图，△ABC内接于⊙O，AB是⊙O的直径，直线AE是⊙O的切线，CD平分∠ACB，若∠CAE=21°，则∠BFC的度数为（ ）| A、66° | B、111° | C、114° | D、119° |
如图，AC是⊙O的切线，C是切点，线段OA交⊙O于点B，且OB=AB，点P是⊙O上的一个动点，那么∠CAP的最大值是（ ）| A、90° | B、30° | C、120° | D、60° |
如图，AB是⊙O的直径，PD切⊙O于点C，交AB的延长线于D，且CO=CD，则∠CAB的度数是（ ）| A、22.5° | B、45° | C、60° | D、30° |
如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，⊙O为△ABC的内切圆，点D是斜边AB的中点，则cos∠ODA=（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知两圆半径分别为3cm，5cm，圆心距为7cm，则这两圆的位置关系为（ ）
| A、相交 | B、外切 | C、内切 | D、外离 |
若两圆的半径分别是2和3，圆心距为5，则这两圆的位置关系是（ ）
| A、内切 | B、相交 | C、外切 | D、外离 |
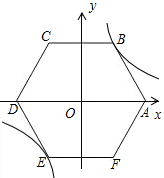如图，在平面直角坐标系中，边长为6的正六边形ABCDEF的对称中心与原点O重合，点A在x轴上，点B在反比例函数y=