Question

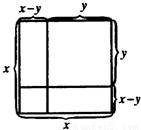
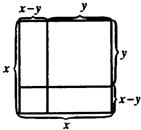17、请你观察右边图形，依据图形面积间的关系，不需要添加辅助线，便可得到一个你非常熟悉的公式，这个公式是

（x+y）（x-y）=x²-y²，x²-y²=（x+y）（x-y）或（x-y）²=x²-2xy+y²

．

Answer 1

分析：本题可通过图中几个图形的面积的关系来进行推导．

解答：解：由图可知，左下角的小正方形的面积=大正方形的面积-两个长x，宽y的矩形的面积和+这两个矩形的重叠部分的面积=x²-2xy+y²，小正方形的面积为（x-y）²，
因此，（x-y）²=x²-2xy+y²，
图中，L形状的图形的面积=大正方形的面积-左上边的边长为y的小正方形的面积=x²-y²，
L状图形的面积=长x宽x-y的矩形的面积+长y宽x-y的矩形的面积=x（x-y）+y（x-y）=（x+y）（x-y），
因此，x²-y²=9x+y）（x-y）．
故本题答案为：（x+y）（x-y）=x²-y²，x²-y²=（x+y）（x-y）或（x-y）²=x²-2xy+y²．

点评：本题考查了完全平方公式和平方差公式的推导过程，运用图形的面积表示是解题的关键．