题目内容
(2002•济南)请你观察右边图形,依据图形面积间的关系,不需要添加辅助线,便可得到一个你非常熟悉的公式,这个公式是 .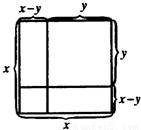
【答案】分析:本题可通过图中几个图形的面积的关系来进行推导.
解答:解:由图可知,左下角的小正方形的面积=大正方形的面积-两个长x,宽y的矩形的面积和+这两个矩形的重叠部分的面积=x2-2xy+y2,小正方形的面积为(x-y)2,
因此,(x-y)2=x2-2xy+y2,
图中,L形状的图形的面积=大正方形的面积-左上边的边长为y的小正方形的面积=x2-y2,
L状图形的面积=长x宽x-y的矩形的面积+长y宽x-y的矩形的面积=x(x-y)+y(x-y)=(x+y)(x-y),
因此,x2-y2=9x+y)(x-y).
故本题答案为:(x+y)(x-y)=x2-y2,x2-y2=(x+y)(x-y)或(x-y)2=x2-2xy+y2.
点评:本题考查了完全平方公式和平方差公式的推导过程,运用图形的面积表示是解题的关键.
解答:解:由图可知,左下角的小正方形的面积=大正方形的面积-两个长x,宽y的矩形的面积和+这两个矩形的重叠部分的面积=x2-2xy+y2,小正方形的面积为(x-y)2,
因此,(x-y)2=x2-2xy+y2,
图中,L形状的图形的面积=大正方形的面积-左上边的边长为y的小正方形的面积=x2-y2,
L状图形的面积=长x宽x-y的矩形的面积+长y宽x-y的矩形的面积=x(x-y)+y(x-y)=(x+y)(x-y),
因此,x2-y2=9x+y)(x-y).
故本题答案为:(x+y)(x-y)=x2-y2,x2-y2=(x+y)(x-y)或(x-y)2=x2-2xy+y2.
点评:本题考查了完全平方公式和平方差公式的推导过程,运用图形的面积表示是解题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
(2002•济南)某校从甲、乙两名优秀选手中选1名选手参加全市中学生田径百米比赛.该校预先对这两名选手测试了8次,测试成绩如下表:
根据测试成绩,请你运用所学过的统计知识做出判断,派哪一位选手参加比赛更好,为什么?
| 测试次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 选手甲的成绩 | 12.1 | 12.2 | 13 | 12.5 | 13.1 | 12.5 | 12.4 | 12.2 |
| 选手乙的成绩 | 12 | 12.4 | 12.8 | 13 | 12.2 | 12.8 | 12.3 | 12.5 |
(2002•济南)如图,⊙O表示一圆形纸板,根据要求,需通过多次剪裁,把它剪成若干个扇形面.操作过程如下:第1次剪裁,将圆形纸板等分为4个扇形;第2次剪裁,将上次得到的扇形面中的一个再等分成4个扇形;以后按第2次剪裁的作法进行下去.
(1)请你在⊙O中,用尺规作出第2次剪裁后得到的7个扇形(保留痕迹,不写作法)
(2)请你通过操作和猜想,将第3、第4和第n次裁剪后所得扇形的总个数(s)填入下表.
(3)请你推断,能不能按上述操作过程,将原来的圆形纸板剪成33个扇形?为什么?

(1)请你在⊙O中,用尺规作出第2次剪裁后得到的7个扇形(保留痕迹,不写作法)
(2)请你通过操作和猜想,将第3、第4和第n次裁剪后所得扇形的总个数(s)填入下表.
| 等分圆及扇形面的次数(n) | 1 | 2 | 3 | 4 | … | n |
| 所得扇形的总个数(S) | 4 | 7 | … |


