题目内容
计算:
(1)4×(-3)2-15÷(-3)-50;
(2)50°24′×3+98°12′25″÷5
(3)化简关于x的代数式(2x2+x)-[kx2-(3x2-x+1)].当k取何值时,代数式的值是常数.
(4)已知A=3b2-2a2,B=ab-2b2-a2.求A-2B的值,其中a=2,b=- .
.
解:(1)原式=4×9+5-50
=-9;
(2)原式=151°12′+19°38′29″
=170°50′29″;
(3)原式=2x2+x-kx2+3x2-x+1
=(5-k)x2+1,
当5-k=0时,即k=5时,
代数式的值为常数;
(4)由已知A-2B=3b2-2a2-2(ab-2b2-a2)
=3b2-2a2-2ab+4b2+2a2
=7b2-2ab,
当a=2,b=- 时,
时,
A-2B=7×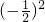 -2×2×(-
-2×2×(- )
)
=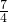 +2
+2
=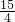 .
.
分析:(1)根据数的乘方运算及有理数的乘除加减运算解答;
(2)根据度分秒的换算计算即可;
(3)去括号、合并同类项,根据化简得到的代数式讨论得出k的取值;
(4)整体代入A-2B再去括号、合并同类项,然后代入求值.
点评:此题考查的知识点是整式的加减、有理数的混合运算及度分秒的计算,关键是要求学生正确按法则运算.
=-9;
(2)原式=151°12′+19°38′29″
=170°50′29″;
(3)原式=2x2+x-kx2+3x2-x+1
=(5-k)x2+1,
当5-k=0时,即k=5时,
代数式的值为常数;
(4)由已知A-2B=3b2-2a2-2(ab-2b2-a2)
=3b2-2a2-2ab+4b2+2a2
=7b2-2ab,
当a=2,b=-
 时,
时,A-2B=7×
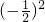 -2×2×(-
-2×2×(- )
)=
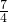 +2
+2=
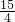 .
.分析:(1)根据数的乘方运算及有理数的乘除加减运算解答;
(2)根据度分秒的换算计算即可;
(3)去括号、合并同类项,根据化简得到的代数式讨论得出k的取值;
(4)整体代入A-2B再去括号、合并同类项,然后代入求值.
点评:此题考查的知识点是整式的加减、有理数的混合运算及度分秒的计算,关键是要求学生正确按法则运算.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目