题目内容
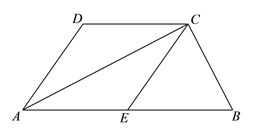
【题目】如图,已知△ACB中,∠ACB=90°,CE是△ACB的中线,分别过点A、点C作CE和AB的平行线,交于点D.
(1)求证:四边形ADCE是菱形;
(2)若CE=4,且∠DAE=60°,求△ACB的面积.
【答案】(1)见解析;(2)![]()
【解析】(1)由AD//CE,CD//AE ,得四边形AECD为平行四边形,根据直角三角形斜边上中线性质,得CE=AE,可知四边形ADCE是菱形;(2)由(1)可知,当∠DAE=60°时,∠CAE=30°,可求AB,再根据三角函数求AC,BC,最后求面积.
(1)证明:∵AD//CE,CD//AE
∴四边形AECD为平行四边形
∵∠ACB=90°,CE是△ACB的中线
∴CE=AE
∴四边形ADCE是菱形
(2)解:∵CE=4,AE= CE=EB
∴AB=8,AE=4
∵四边形ADCE是菱形,∠DAE=60°
∴∠CAE=30°
∵在Rt△ABC中,∠ACB=90°,∠CAB=30°, AB=8
![]() ,
,![]()
∴AC = ![]()
∴![]()

【题目】某运输部门规定:办理托运,当一种物品的重量不超过16千克时,需付基础费30元和保险费a元:为限制过重物品的托运,当一件物品超过16千克时,除了付以上基础费和保险费外,超过部分每千克还需付b元超重费.设某件物品的重量为x千克.
(1)当x≤16时,支付费用为__________________元(用含a的代数式表示);
当x≥16时,支付费用为_________________元(用含x和a、b的代数式表示);
(2)甲、乙两人各托运一件物品,物品重量和支付费用如下表所示
物品重量(千克) | 支付费用(元) |
18 | 39 |
25 | 53 |
试根据以上提供的信息确定a,b的值.
(3)根据这个规定,若丙要托运一件超过16千克的物品,但支付的费用不想超过70元,那么丙托运的物品最多是多少千克.