题目内容
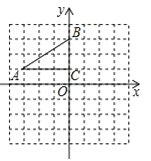
【题目】如图，在平面直角坐标系中，直角△ABC的三个顶点分别是A（﹣3，1），B（0，3），C（0，1）
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C1；
（2）分别连结AB1、BA1后，求四边形AB1A1B的面积．
【答案】（1）作图见解析；（2）12．
【解析】
试题分析：（1）利用网格特点，延长AC到A1使A1C=AC，延长BC到B1使B1C=BC，C点的对应点C1与C点重合，则△A1B1C1满足条件；
（2）四边形AB1A1B的对角线互相垂直平分，则四边形AB1A1B为菱形，然后利用菱形的面积公式计算即可．
试题解析：（1）如图，△A1B1C1为所作：
（2）四边形AB1A1B的面积=
×6×4=12．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】一段时间内，某商场销售某品牌的女装30件，各种尺码的销售量如下表：
尺码（cm） | 155 | 160 | 165 | 170 | 175 |
销售量（件） | 2 | 10 | 12 | 4 | 2 |
则这30件女装尺码的众数和中位数分别是（ ）
A.175cm，165cm
B.165cm，165cm
C.165cm，175cm
D.165cm，170cm
【题目】根据下面表格中的对应值：
x | 3.24 | 3.25 | 3.26 |
ax2+bx+c | ﹣0.02 | 0.01 | 0.03 |
判断关于x的方程ax2+bx+c＝0（a≠0）的一个解x的范围是（ ）
A. x＜3.24B. 3.24＜x＜3.25C. 3.25＜x＜3.26D. x＞3.26
