Question

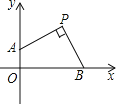
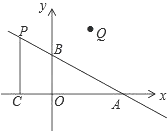
【题目】如图，在平面直角坐标系中，O是坐标原点，点A的坐标为（4，0），点B的坐标为（0，b）（b＞0），点P是直线AB上位于第二象限内的一个动点，过点P作PC⊥x轴于点C，记点P关于y轴的对称点为Q，设点P的横坐标为a．

（1）当b=3时，

①求直线AB的解析式；

②若QO=QA，求P点的坐标．

（2）是否同时存在a、b，使得△QAC是等腰直角三角形？若存在，求出所有满足条件的a、b的值；若不存在，请说明理由．

Answer 1

【答案】（1）y=-x+3；P坐标得P（-2，）；（2）a=-4，b=4或a=-，b=2．

【解析】

试题分析：（1）①由题意确定出B坐标，设直线AB解析式为y=kx+b，把A与B坐标代入求出k与b的值，即可求出AB解析式；②由AQ=QO以及OA的长，确定出Q横坐标，根据P与Q关于y轴对称，得出P横坐标，代入直线AB解析式求出纵坐标，即可确定出P坐标；

（2）同时存在a、b，使得△QAC是等腰直角三角形，分两种情况考虑：①若∠QAC=90°；②若∠AQC=90°，分别求出a与b的值即可．

试题解析：（1）①由A（4，0），B（0，3），

设直线AB解析式为y=kx+b，

把A与B坐标代入得：，

解得：k=-，b=3，

则直线AB解析式为y=-x+3；

②∵QA=QO，OA=4，

∴xQ=2，

∵点P关于y轴的对称点为Q，

∴xP=-2，

代入直线AP解析式得-×（-2）+3=，

则P坐标得P（-2，）；

（2）①若∠QAC=90°，如图1所示，

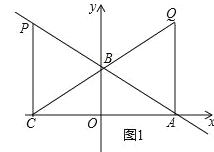
∴xQ=4，

∴a=xP=-4，

∴AC=AQ=8，即P（-4，8），

∴直线AP解析式为y=-x+4，

∴a=-4，b=4；

②若∠AQC=90°，如图2所示，

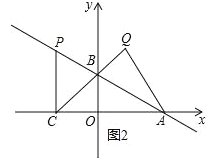
则AC=4-a=2CH=-4a，

∴a=-，

∴xP=-，yP=yq=，即P（-，），

∴直线AP解析式为y=-x+2，

∴a=-，b=2，

综上所示，a=-4，b=4或a=-，b=2．