题目内容
【题目】如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,AE=BD,∠B=∠CED,AE=3,DE=![]() ,则线段CE的长为_____.
,则线段CE的长为_____.

【答案】5
【解析】
过点C作CF//DE交AB的延长线于点F,设CE=x,CF=y,由DE//FC可得![]() ,可表示BF=
,可表示BF=![]() .证明△ADE∽△CFB,可得
.证明△ADE∽△CFB,可得![]() ,得出x与y的关系式①,可得
,得出x与y的关系式①,可得![]() ,则可得出x与y的关系式②,联立①②可解出x得出答案.
,则可得出x与y的关系式②,联立①②可解出x得出答案.
解:过点C作CF//DE交AB的延长线于点F,
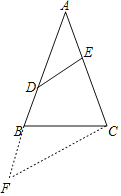
∵AB=AC,AE=BD,
∴AD=CE,
设CE=x,CF=y,
∵DE//FC,
∴![]() ,
,
∴![]() ,
,
∴BF=![]() .
.
∵∠ABC=∠CED,
∴∠AED=∠CBF,
∵DE//CF,
∴∠ADE=∠BFC,
∴△ADE∽△CFB,
∴![]() ,
,
∴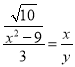 .
.
∴![]() ①
①
∵DE//CF,
∴△ADE∽△AFC,
∴![]() ,
,
∴![]() ,
,
∴![]() ②.
②.
由①②可得,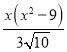 =
=![]() .
.
整理得x2﹣3x﹣10=0.
解得x=5,x=﹣2(舍去).
故答案为:5.

练习册系列答案
相关题目