题目内容
【题目】(1)已知: ![]() ,
, ![]() 求作:
求作: ![]() ,使得
,使得![]() ,
, ![]() .
.
 作图:
作图:
(2)如图,已知![]() ,求作射线OC,使OC平分
,求作射线OC,使OC平分![]() .
.
作射线OC;
在OA和OB上分别截取OD,OE,使OD=OE;
分别以点D,E为圆心,以大于![]() 长为半径,
长为半径,
在![]() 内作弧,两弧交于点C.上述做法合理的顺序是_____________.(写序号)
内作弧,两弧交于点C.上述做法合理的顺序是_____________.(写序号)

这样做出的射线OC就是∠O 的角平分线,其依据是___________________.
【答案】(1)见解析;(2)②③①,三边分别相等的两个三角形全等,全等三角形的对应角相等.
【解析】试题分析:(1)①作∠EBC=∠α,②在射线BE上截取BA=m,在射线BF上截取BC=n,连接AC.△ABC即为所求;
(2)先根据角平分线的作法进行判断,再根据图形进行说理,运用全等三角形的判定与性质进行证明,进而得出结论.
试题解析:(1)如图,①作∠EBC=∠α,②在射线BE上截取BA=m,在射线BF上截取BC=n,连接AC.△ABC即为所求.
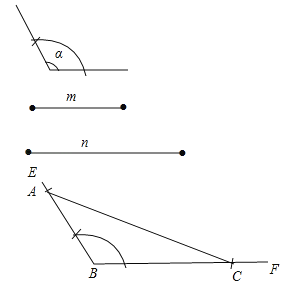
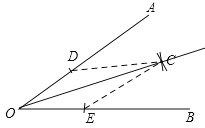
(2)解:已知∠AOB,求作射线OC,使OC平分∠AOB.
步骤为:
第一步:在OA和OB上分别截取OD,OE,使OD=OE;
第二步:分别以D,E为圆心,大于![]() DE的长为半径作弧,在∠AOB内,两弧交于C;
DE的长为半径作弧,在∠AOB内,两弧交于C;
第三步:作射线OC.
故作法合理的顺序为②③①.
如图所示,连接CD,CE,由题可得,OD=OE,CD=CE,在△OCD和△OCE中,∵OD=OE,CD=CE,OC=OC,∴△OCD≌△OCE(SSS),∴∠COD=∠COE(全等三角形的对应角相等),∴OC是∠AOB的平分线(角平分线定义).
故答案为:②③①,三边分别相等的两个三角形全等,全等三角形的对应角相等.

练习册系列答案
相关题目