题目内容
(2010•潮阳区模拟)如图1,点A、B是双曲线y= (k>0)上的点,分别经过A、B两点向x轴、y轴作垂线段AC、AD、BE、BF,AC和BF交于点G,得到正方形OCGF(阴影部分),且S阴影=1,△AGB的面积为2.
(k>0)上的点,分别经过A、B两点向x轴、y轴作垂线段AC、AD、BE、BF,AC和BF交于点G,得到正方形OCGF(阴影部分),且S阴影=1,△AGB的面积为2.
(1)求双曲线的解析式;
(2)在双曲线上移动点A和点B,上述作图不变,得到矩形OCGF(阴影部分),点A、B在运动过程中始终保持S阴影=1不变(如图2),则△AGB的面积是否会改变?说明理由.
【答案】分析:(1)由于正方形OCGF的面积是1,得出OC=CG=1,即点A的横坐标为1,点B纵坐标为1.由点A、B是双曲线y=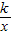 上的点,得出点A的纵坐标与点B的横坐标都是k,从而可用含k的代数式表示AG,BG,再根据△AGB的面积为2,列出关于k的方程,求解即可;
上的点,得出点A的纵坐标与点B的横坐标都是k,从而可用含k的代数式表示AG,BG,再根据△AGB的面积为2,列出关于k的方程,求解即可;
(2)由于△AGB的面积= AG•BG,所以本题即求
AG•BG,所以本题即求 AG•BG的值是否为一个常数.为此,设矩形OCGF的边OC=m,则点A的横坐标为m,由S阴影=OC•OF=1,可知OF=
AG•BG的值是否为一个常数.为此,设矩形OCGF的边OC=m,则点A的横坐标为m,由S阴影=OC•OF=1,可知OF= ,即点B纵坐标为
,即点B纵坐标为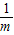 .然后由点A、B是双曲线y=
.然后由点A、B是双曲线y=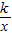 上的点,得出点A的纵横坐标与点B的横坐标,从而可用含m的代数式表示AG,BG,进而求出
上的点,得出点A的纵横坐标与点B的横坐标,从而可用含m的代数式表示AG,BG,进而求出 AG•BG的值,从而得出结果.
AG•BG的值,从而得出结果.
解答:解:(1)∵四边形OCGF是正方形,
∴OC=CG=GF=OF,∠CGF=90°,
∵OC2=S阴影=1,
∴OC=CG=GF=OF=1,
∴点A的横坐标为1,点B纵坐标为1.
∵点A、B是双曲线y=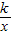 上的点,
上的点,
∴点A的纵坐标为y=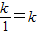 ,点B横坐标为x=
,点B横坐标为x=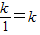 ,
,
∴AC=k,BF=k,
∴AG=k-1,BG=k-1.
∵∠AGB=∠CGF=90°,
∴S△AGB= AG•BG=
AG•BG=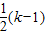 2=2,
2=2,
解得k=3(取正值).
∴反比例函数的解析式为y=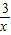 ;
;
(2)点A、B在运动过程中△AGB的面积保持不变.
理由如下:
设矩形OCGF的边OC=m.
∵S阴影=OC•OF=1,∴OF=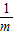 .
.
∴点A的横坐标为m,点B纵坐标为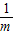 .
.
∵点A、B是双曲线y=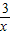 上的点,
上的点,
∴点A的纵横坐标为y=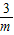 ,点B横坐标为
,点B横坐标为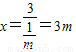 .
.
∴AC=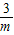 ,BF=3m.
,BF=3m.
又FG=OC=m,CG=OF=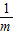 ,
,
∴AG=AC-CG=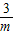 -
-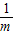 =
=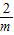 ,BG=BF-FG=3m-m=2m,
,BG=BF-FG=3m-m=2m,
∴S△AGB= AG•BG=
AG•BG= •
•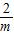 •2m=2.
•2m=2.
∴点A、B在运动过程中△AGB的面积保持不变.
点评:本题考查了反比例函数的图象的性质以及正方形、矩形的性质,利用形数结合解决此类问题,是非常有效的方法.
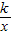 上的点,得出点A的纵坐标与点B的横坐标都是k,从而可用含k的代数式表示AG,BG,再根据△AGB的面积为2,列出关于k的方程,求解即可;
上的点,得出点A的纵坐标与点B的横坐标都是k,从而可用含k的代数式表示AG,BG,再根据△AGB的面积为2,列出关于k的方程,求解即可;(2)由于△AGB的面积=
 AG•BG,所以本题即求
AG•BG,所以本题即求 AG•BG的值是否为一个常数.为此,设矩形OCGF的边OC=m,则点A的横坐标为m,由S阴影=OC•OF=1,可知OF=
AG•BG的值是否为一个常数.为此,设矩形OCGF的边OC=m,则点A的横坐标为m,由S阴影=OC•OF=1,可知OF= ,即点B纵坐标为
,即点B纵坐标为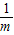 .然后由点A、B是双曲线y=
.然后由点A、B是双曲线y=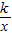 上的点,得出点A的纵横坐标与点B的横坐标,从而可用含m的代数式表示AG,BG,进而求出
上的点,得出点A的纵横坐标与点B的横坐标,从而可用含m的代数式表示AG,BG,进而求出 AG•BG的值,从而得出结果.
AG•BG的值,从而得出结果.解答:解:(1)∵四边形OCGF是正方形,
∴OC=CG=GF=OF,∠CGF=90°,
∵OC2=S阴影=1,
∴OC=CG=GF=OF=1,
∴点A的横坐标为1,点B纵坐标为1.
∵点A、B是双曲线y=
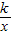 上的点,
上的点,∴点A的纵坐标为y=
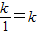 ,点B横坐标为x=
,点B横坐标为x=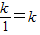 ,
,∴AC=k,BF=k,
∴AG=k-1,BG=k-1.
∵∠AGB=∠CGF=90°,
∴S△AGB=
 AG•BG=
AG•BG=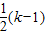 2=2,
2=2,解得k=3(取正值).
∴反比例函数的解析式为y=
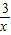 ;
;(2)点A、B在运动过程中△AGB的面积保持不变.
理由如下:
设矩形OCGF的边OC=m.
∵S阴影=OC•OF=1,∴OF=
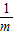 .
.∴点A的横坐标为m,点B纵坐标为
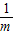 .
.∵点A、B是双曲线y=
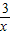 上的点,
上的点,∴点A的纵横坐标为y=
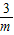 ,点B横坐标为
,点B横坐标为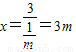 .
.∴AC=
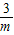 ,BF=3m.
,BF=3m.又FG=OC=m,CG=OF=
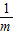 ,
,∴AG=AC-CG=
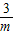 -
-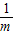 =
=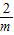 ,BG=BF-FG=3m-m=2m,
,BG=BF-FG=3m-m=2m,∴S△AGB=
 AG•BG=
AG•BG= •
•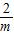 •2m=2.
•2m=2.∴点A、B在运动过程中△AGB的面积保持不变.
点评:本题考查了反比例函数的图象的性质以及正方形、矩形的性质,利用形数结合解决此类问题,是非常有效的方法.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 x
x 分别与x轴、y轴交于点C和点D,一组抛物线的顶点A1,A2,A3,…,An,依次是直线CD上的点,这组抛物线与x轴的交点依次是B1,B2,B3,…,Bn-1,Bn,且OB1=B1B2=B2B3=…=Bn-1Bn,点A1坐标(1,1),则点An坐标为 .
分别与x轴、y轴交于点C和点D,一组抛物线的顶点A1,A2,A3,…,An,依次是直线CD上的点,这组抛物线与x轴的交点依次是B1,B2,B3,…,Bn-1,Bn,且OB1=B1B2=B2B3=…=Bn-1Bn,点A1坐标(1,1),则点An坐标为 .

