题目内容
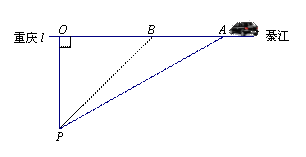
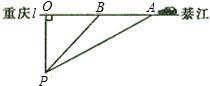据交管部门统计，高速公路超速行驶是引发交通事故的主要原因．我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速，渝黔高速公路某路段的限速是：每小时80千米（即最高时速不超过80千米），如图，他们将观测点设在到公路l的距离为0.1千米的P处．这时，一辆轿车由綦江向重庆匀速直线驶来，测得此车从A处行驶到B处所用的时间为3秒（注：3秒=| 1 | 1200 |
分析：在直角△OAP中，直角△OBP中，利用三角函数即可求得OA，OB，求得AB的长，即可求解．
解答：解：设该轿车的速度为每小时x千米．
∵AB=AO-BO，∠BPO=45°，
∴BO=PO=0.1千米． （2分）
又AO=OP×tan59°=0.1×1.6643=0.16643（千米），（3分）
∴AB=AO-BO=0.16643-0.1=0.1×0.6643=0.06643（千米），（1分）
即AB≈0.066千米． （1分）
3秒=
小时，
∴x=0.06643×1200≈79.716千米/时． （2分）
∵79.716＜80，
∴该轿车没有超速． （1分）
解：设该轿车的速度为每小时x千米．∵AB=AO-BO，∠BPO=45°，
∴BO=PO=0.1千米． （2分）
又AO=OP×tan59°=0.1×1.6643=0.16643（千米），（3分）
∴AB=AO-BO=0.16643-0.1=0.1×0.6643=0.06643（千米），（1分）
即AB≈0.066千米． （1分）
3秒=
| 1 |
| 1200 |
∴x=0.06643×1200≈79.716千米/时． （2分）
∵79.716＜80，
∴该轿车没有超速． （1分）
点评：本题是把实际问题转化为解直角三角形的问题，考查三角函数定义的应用．
练习册系列答案
名校课堂系列答案
相关题目
小时），并测得∠APO＝59°，