题目内容
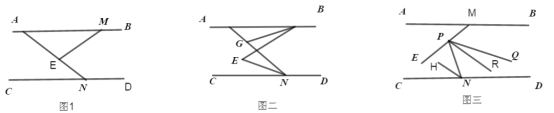
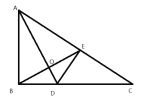
【题目】如图,将△ABC沿直线AD折叠,点B与点E重合,连接BE交AD于O.∠ABC=90°,AB=6,BC=8,AC=10,SACD=15.有下列结论:①SCDE=5;②CD=5;③OB=OE;④SABD:SACD=3:4,则以上结论正确的是( )
A. ①②B. ②③C. ②③④D. ①②③
【答案】B
【解析】
由题意可得△ABD≌△AED,∠AED=∠ABC=90°,AE=AB=6,则CE=4,由SACD=15可得DE=3,即可求得SCDE; 由BD= DE=3,可得CD=BC-BD=5;由△ABD≌△AED得∠BAD=∠CAD,AB=AE,由等腰三角形三线合一可得OB=OE;由SABD=![]() ,可得SABD:SACD=9:15=3:5.
,可得SABD:SACD=9:15=3:5.
解: ∵△ABC沿直线AD折叠,点B与点E重合,
∴△ABD≌△AED,
∴∠AED=∠ABC=90°,AE=AB=6,BD= DE,
∵SACD=![]() =15,AC=10,
=15,AC=10,
∴BD= DE=3,CE=AC-AE=4,
∴SCDE =![]() ,故①错误;
,故①错误;
∵△ABD≌△AED,
∴BD= DE=3,
∴CD=BC-BD=8-3=5,故②正确;
∵△ABD≌△AED,
∴∠BAD=∠CAD,AB=AE,
∴OB=OE,故③正确;
∵SABD=![]() ,SACD=15,
,SACD=15,
∴SABD:SACD=9:15=3:5,故④错误.
故以上结论正确的是②③.
故选B.

【题目】延庆区由于生态质量良好、自然资源丰富,成为北京的生态涵养区,是其生态屏障和水源保护地.为降低空气污染,919公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型 | B型 | |
价格(万元/台) | a | b |
年载客量(万人/年) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.