Question

OM是一堵高为2.5米的围墙的截面，小鹏从围墙外的A点向围墙内抛沙包，但沙包抛出后正好打在了横靠在围墙上的竹竿CD的B点处，经过的路线是二次函数图像的一部分，如果沙包不被竹竿挡住，将通过围墙内的E点，现以O为原点，单位长度为1，建立如图所示的平面直角坐标系，E点的坐标(3，)，点B和点E关于此二次函数的对称轴对称，若tan∠OCM=1(围墙厚度忽略不计)。 

(1)求CD所在直线的函数表达式；

(2)求B点的坐标；

(3)如果沙包抛出后不被竹竿挡住，会落在围墙内距围墙多远的地方?

Answer 1

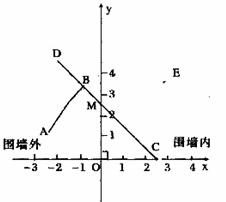
解：(1)∵OM=2.5，tan∠OCM=1，

        ∴∠OCM=，OC=OM=2.5。

        ∴C(2.5，0)，M(0，2.5)。

    设CD的解析式为y=kx+2.5 (k≠o)，

       2.5k+2.5=0，

       k= 一1。

    ∴y= ―x+2.5。      

  (2)∵B、E关于对称轴对称，∴B(x，)。 

    又∵B在y=一x+2.5上，∴x= 一l。

    ∴B(―1，)。

  (3)抛物线y=经过B(一1，)，E(3，)，

∴

  

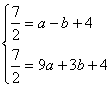
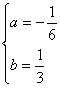
    ∴y=，

    令y=o，则=0，解得或。

  所以沙包距围墙的距离为6米。