题目内容
 先填写完成第(1)小题中的空缺部分(数学表达式或理由),再按要求解答第(2)小题.
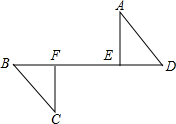
先填写完成第(1)小题中的空缺部分(数学表达式或理由),再按要求解答第(2)小题.如图:AD=CB,AE⊥BD,CF⊥BD,垂足分别是E、F,DF=BE.
(1)求证:∠D=∠B;
(2)请你连结AB、CD,探究AB与CD有何位置关系?并证明你的结论.
证明:(1)∵AE⊥BD,CF⊥BD,
∴∠AED=∠
CFB
CFB
=90°,∵DF=BE,
∴DF-
EF
EF
=BE-EF
EF
,即DE=BF.
在Rt△ADE和Rt△CBF中,
方程组:
∴Rt△ADE≌Rt△CBF
HL
HL
,∴∠D=∠B
全等三角形的对应角相等
全等三角形的对应角相等
.(2)
分析:(1)通过全等三角形的判定定理HL证得Rt△ADE≌Rt△CBF,则该全等三角形的对应角相等:∠D=∠B;
(2)利用(1)中的结论可以推知AD∥BC,又AD=BC,则四边形ABCDF是平行四边形,则AB∥CD.
(2)利用(1)中的结论可以推知AD∥BC,又AD=BC,则四边形ABCDF是平行四边形,则AB∥CD.
解答: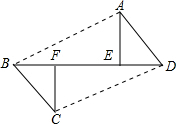 (1)证明:如图,∵AE⊥BD,CF⊥BD,
(1)证明:如图,∵AE⊥BD,CF⊥BD,
∴∠AED=∠CBF=90°.
又∵DF=BE,
∴DF-EF=BE-EF,即DE=BF.
∴在Rt△DEA与Rt△BFC中,
,
∴Rt△ADE≌Rt△CBF(HL),
∴∠D=∠B(全等三角形的对应角相等);
故答案是:CFB;EF;EF;HL;全等三角形的对应角相等;
(2)AB与CD相互平行.理由如下:
如图,连接AB、CD.
∵由(1)知,∠D=∠B,
∴AD∥BC.
又∵AD=BC,
∴四边形ABCDF是平行四边形,
∴AB∥CD.
 (1)证明:如图,∵AE⊥BD,CF⊥BD,
(1)证明:如图,∵AE⊥BD,CF⊥BD,∴∠AED=∠CBF=90°.
又∵DF=BE,
∴DF-EF=BE-EF,即DE=BF.
∴在Rt△DEA与Rt△BFC中,
|
∴Rt△ADE≌Rt△CBF(HL),
∴∠D=∠B(全等三角形的对应角相等);
故答案是:CFB;EF;EF;HL;全等三角形的对应角相等;
(2)AB与CD相互平行.理由如下:
如图,连接AB、CD.
∵由(1)知,∠D=∠B,
∴AD∥BC.
又∵AD=BC,
∴四边形ABCDF是平行四边形,
∴AB∥CD.
点评:本题考查了全等三角形的判定与性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


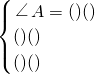
 先填写完成第(1)小题中的空缺部分(数学表达式或理由),再按要求解答第(2)小题.
先填写完成第(1)小题中的空缺部分(数学表达式或理由),再按要求解答第(2)小题.