题目内容
先填写完成第(1)小题中的空缺部分(数学表达式或理由),再按要求解答第(2)小题.
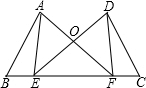
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)请你连接AE、DF.问AE和DF相等吗?为什么?
证明:
(1)∵BE=CF(已知),
∴BE+EF=CF+EF(
即BF=CE.
在△ABF和△DCE中,
∴△ABF≌△DCE
∴AB=DC
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;

(2)请你连接AE、DF.问AE和DF相等吗?为什么?
证明:
(1)∵BE=CF(已知),
∴BE+EF=CF+EF(
等式的性质
等式的性质
),即BF=CE.
在△ABF和△DCE中,
|
∴△ABF≌△DCE
(AAS)
(AAS)
,∴AB=DC
(全等三角形的对应边相等)
(全等三角形的对应边相等)
.分析:(1)求出BF=CE,根据AAS推出△ABF≌△DCE即可;
(2)根据SAS证△ABE≌△DCF,根据全等三角形的性质推出即可.
(2)根据SAS证△ABE≌△DCF,根据全等三角形的性质推出即可.
解答:证明:(1)∵BE=CF,
∴BE+EF=CF+EF(等式的性质),
即BF=CE,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(AAS),
∴AB=DC(全等三角形的对应边相等).
故答案为:(等式的性质),∠D,已知,∠B=∠C,BF=CE,(全等三角形的对应边相等).
(2)
AE=DF,
证明:∵在△ABE和△DCF中
,
∴△ABE≌△DCF(SAS),
∴AE=DF.
即AE和BF相等.
∴BE+EF=CF+EF(等式的性质),
即BF=CE,
在△ABF和△DCE中,
|
∴△ABF≌△DCE(AAS),
∴AB=DC(全等三角形的对应边相等).
故答案为:(等式的性质),∠D,已知,∠B=∠C,BF=CE,(全等三角形的对应边相等).
(2)

AE=DF,
证明:∵在△ABE和△DCF中
|
∴△ABE≌△DCF(SAS),
∴AE=DF.
即AE和BF相等.
点评:本题考查了全等三角形的性质和判定,主要考查学生的推理能力.

练习册系列答案
相关题目
 先填写完成第(1)小题中的空缺部分(数学表达式或理由),再按要求解答第(2)小题.
先填写完成第(1)小题中的空缺部分(数学表达式或理由),再按要求解答第(2)小题.
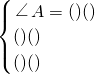
 先填写完成第(1)小题中的空缺部分(数学表达式或理由),再按要求解答第(2)小题.
先填写完成第(1)小题中的空缺部分(数学表达式或理由),再按要求解答第(2)小题.