Question

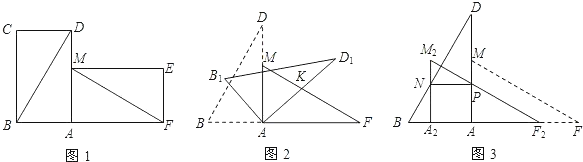
【题目】已知：如图①，在ABCD中，O为对角线BD的中点．过O的直线MN交直线AB于点M，交直线CD于点N；过O的另一条直线PQ交直线AD于点P，交直线BC于点Q，连接PN、MQ．

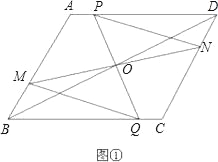
（1）试证明△PON与△QOM全等；

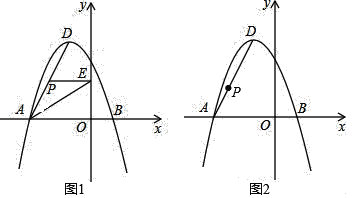
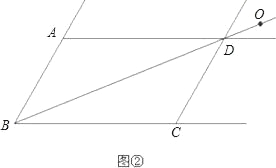
（2）若点O为直线BD上任意一点，其他条件不变，则△PON与△QOM又有怎样的关系？试就点O在图②所示的位置，画出图形，证明你的猜想；

（3）若点O为直线BD上任意一点（不与点B、D重合），设OD：OB＝k，PN＝x，MQ＝y，则y与x之间的函数关系式为　 　．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）见解析.

【解析】

（1）根据平行四边形的性质容易得到全等条件证明△DOP≌△BOQ，△PON≌△QOM，然后利用全等三角形的性质得到PO=QO，MO=NO，然后再证明△PON≌△QOM就可以解决问题；
（2）点O为直线BD上任意一点，则△MOQ∽△NOP．根据AP∥BQ，BM∥CN可以得到比例线段，而∠NOP=∠MOQ，可以证明△MOQ∽△NOP了；
（3）根据（2）和已知可以得到==，根据这个等式可以求出y与x之间的函数关系式．

（1）证明：在平行四边形ABCD中，AD∥BC，

∴∠PDO＝∠QBO．

∵∠DOP＝∠BOQ，DO＝BO，

∴△DOP≌△BOQ．

∴PO＝QO．

同理MO＝NO．

∵∠PON＝∠QOM，

∴△PON≌△QOM．

（2）解：画图如图所示．

△MOQ∽△NOP．

∵AP∥BQ，BM∥CN，

∴OD：OB＝OP：OQ，OD：OB＝ON：OM．

∴OP：OQ＝ON：OM．

∴∠NOP＝∠MOQ．

∴△MOQ∽△NOP．

（3）解：根据（2）和已知可以得到==，

∵OD：OB＝k，PN＝x，MQ＝y，

∴y＝．