Question

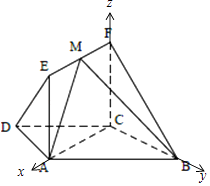
【题目】如图，在等腰梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD， ．
（1）求证：BC⊥平面ACFE；
（2）点M在线段EF上运动，设平面MAB与平面FCB二面角的平面角为θ（θ≤90°），试求cosθ的取值范围．

Answer 1

【答案】
（1）证明：在梯形ABCD中，

∵AB∥CD，AD=DC=CB=1，∠ABC=60°，

∴AB=2，则AC2=AB2+BC2﹣2ABBCcos60°=3，

∴AB2=AC2+BC2，得BC⊥AC．

∵平面ACFE⊥平面ABCD，平面ACFE∩平面ABCD=AC，

BC平面ABCD，

∴BC⊥平面ACFE

（2）解：由（1）可建立分别以直线CA，CB，CF为x轴，y轴，z轴的如图所示空间直角坐标系，

令FM=λ（0≤λ≤ ），则C（0，0，0），A（ ，0，0），B（0，1，0），M（λ，0，1）．

=（﹣ ，1，0）， =（λ，﹣1，1）．

设 =（x，y，z）为平面MAB的一个法向量，

由 ，取x=1，得 =（1， ， ），

∵ =（1，0，0）是平面FCB的一个法向量．

∴cosθ= = = ．

∵0≤λ≤ ，∴当λ=0时，cosθ有最小值 ，

当λ= 时，cosθ有最大值 ．

∴cosθ∈[ ]．

【解析】（1）由已知求解三角形可得BC⊥AC，由平面ACFE⊥平面ABCD，结合面面垂直的性质得BC⊥平面ACFE；（2）建立空间坐标系，令FM=λ（0≤λ≤ ），根据坐标表示出两个平面的法向量，结合向量的有关运算求出二面角的余弦值关于λ的表达式，再利用函数的有关知识求出余弦的范围．
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点，需要掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题．