题目内容
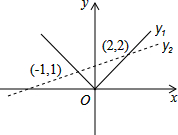 如图所示,函数y1=|x|和y2=
如图所示,函数y1=|x|和y2=| 1 |
| 3 |
| 4 |
| 3 |
分析:首先由已知得出y1=x或y1=-x又相交于(-1,1),(2,2)两点,根据y1>y2列出不等式求出x的取值范围.
解答:解:当x≥0时,y1=x,又,
∴两直线的交点为(2,2),
y2=
x+
当x<0时,y1=-x,又y2=
x+
,
∴两直线的交点为(-1,1),
由图象可知:当y1>y2时x的取值范围为:x<-1或x>2.
故答案为:x<-1或x>2.
∴两直线的交点为(2,2),
y2=
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
∴两直线的交点为(-1,1),
由图象可知:当y1>y2时x的取值范围为:x<-1或x>2.
故答案为:x<-1或x>2.
点评:此题考查的是两条直线相交问题,关键要由已知列出不等式,注意象限和符号.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
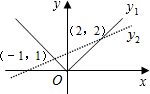 如图所示,函数y1=|x|和y2=
如图所示,函数y1=|x|和y2=| 1 |
| 3 |
| 4 |
| 3 |
| A、x<-1 |
| B、-1<x<2 |
| C、x>2 |
| D、x<-1或x>2 |
 的图象相交于(-1,1),(2,2)两点.当
的图象相交于(-1,1),(2,2)两点.当 时,x的取值范围是 .
时,x的取值范围是 .
 的图象相交于(-1,1),(2,2)两点.当
的图象相交于(-1,1),(2,2)两点.当 时,x的取值范围是 .
时,x的取值范围是 .
 的图象相交于(-1,1),(2,2)两点.当y1>y2时,x的取值范围是( )
的图象相交于(-1,1),(2,2)两点.当y1>y2时,x的取值范围是( )