题目内容
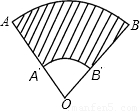
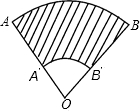 已知:如图,扇形OAB和扇形OA′B′的圆心角相同,设AA′=BB′=d.
已知:如图,扇形OAB和扇形OA′B′的圆心角相同,设AA′=BB′=d. =l1,
=l1,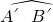 =l2.
=l2.
求证:图中阴影部分的面积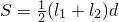 .
.
证明:设∠AOB=n°,OA′=OB′=r,
∵ =l1,
=l1,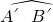 =l2.
=l2.
∴l1=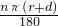 ,l2=
,l2=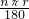 ,
,
∴ =
= ,
,
∴r=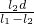 ①,
①,
∵S阴影=S扇形OAB-S扇形OA′B′= l1(r+d)-
l1(r+d)- l2r=
l2r= (l1r+l1d-l2r)
(l1r+l1d-l2r)
= [(l1-l2)r+l1d]
[(l1-l2)r+l1d]
= [(l1-l2)×
[(l1-l2)×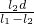 +l1d]
+l1d]
= (l2d+l1d)
(l2d+l1d)
= (l1+l2)d.
(l1+l2)d.
分析:设∠AOB=n°,OA′=OB′=r,根据弧长公式用l1,l2表示出r,再根据S阴影=S扇形OAB-S扇形OA′B′进行计算即可得出结论.
点评:本题考查的是扇形面积的计算及弧长公式,根据弧长公式用l1,l2表示出r的值是解答此题的关键.
∵
 =l1,
=l1,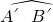 =l2.
=l2.∴l1=
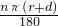 ,l2=
,l2=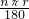 ,
,∴
 =
= ,
,∴r=
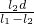 ①,
①,∵S阴影=S扇形OAB-S扇形OA′B′=
 l1(r+d)-
l1(r+d)- l2r=
l2r= (l1r+l1d-l2r)
(l1r+l1d-l2r)=
 [(l1-l2)r+l1d]
[(l1-l2)r+l1d]=
 [(l1-l2)×
[(l1-l2)×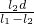 +l1d]
+l1d]=
 (l2d+l1d)
(l2d+l1d)=
 (l1+l2)d.
(l1+l2)d.分析:设∠AOB=n°,OA′=OB′=r,根据弧长公式用l1,l2表示出r,再根据S阴影=S扇形OAB-S扇形OA′B′进行计算即可得出结论.
点评:本题考查的是扇形面积的计算及弧长公式,根据弧长公式用l1,l2表示出r的值是解答此题的关键.

练习册系列答案
相关题目
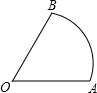 (1997•台湾)已知:如图,扇形AOB.求作:一个与OA、OB、
(1997•台湾)已知:如图,扇形AOB.求作:一个与OA、OB、
 已知:如图,扇形OAB和扇形OA′B′的圆心角相同,设AA′=BB′=d.
已知:如图,扇形OAB和扇形OA′B′的圆心角相同,设AA′=BB′=d.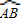 =l1,
=l1, =l2.
=l2.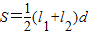 .
.
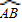 皆相切的圆.
皆相切的圆.