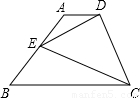
题目内容
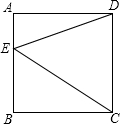
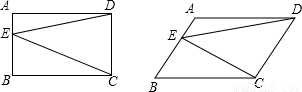
附加题:E是四边形ABCD中AB上一点(E不与A、B重合).?(1)如图,当四边形ABCD是正方形时,△ADE、△BCE和△CDE的面积之间有着怎样的关系?证明你的结论.
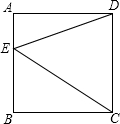
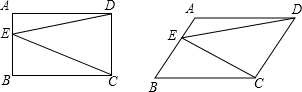
(2)若四边形ABCD是矩形时,(1)中的结论是否仍然成立?为什么?ABCD是平行四边形呢?
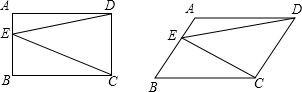
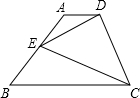
(3)当四边形ABCD是梯形时,(1)中的结论还成立吗?请说明理由.?
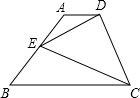
分析:正方形,矩形,平行四边形图形中的三个三角形都是等高的三角形,它们的面积关系,就要看底边的关系了,由于AE+EB=CD,所以S△ADE+S△BCE=S△CDE在这三个图形中都成立;梯形不具备这一特征,就不一定成立.
解答:解:①S△ADE+S△BCE=S△CDE?
方法1:同底同高?
S△ADE+S△BCE=
AE×AD+
EB×AD=
AD(AE+EB)=
AD×AB=S△DEC.
方法2:因为过E作EF∥BC交DC于F,则四边形AEFD和EBCF是矩形
所以S△AED=S△EFD,S△EBC=S△EFC,?
所以S△ADE+S△BCE=S△EFD+S△EFC=S△DEC.
②四边形ABCD是矩形时(1)中结论成立,方法同上
当四边形ABCD是平行四边形时,结论还是成立.
③当四边形ABCD是梯形时,①中结论当E点为AB中点时成立,其它情况不成立不成立.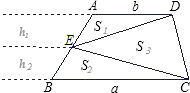
理由如下:
设S△ADE=S1,S△BCE=S2,S△DEC=S3,
梯形ABCD上底为a,下底为b面积为S,如图.
则S1=
bh1;S2=
ah2S3=S-S1-S2=
(a+b)(h1+h2)-
ah2-bh1=
(ah1+bh2)
如果S△ADE+S△BCE=S△DEC,则有
(bh1+ah2)=
(ah1+bh2),a(h1-h2)=b(h1-h2).
如果h1=h2,则E为AB中点,如果h1≠h2,则a=b,四边形ABCD是平行四边形.
方法1:同底同高?
S△ADE+S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
方法2:因为过E作EF∥BC交DC于F,则四边形AEFD和EBCF是矩形
所以S△AED=S△EFD,S△EBC=S△EFC,?
所以S△ADE+S△BCE=S△EFD+S△EFC=S△DEC.
②四边形ABCD是矩形时(1)中结论成立,方法同上
当四边形ABCD是平行四边形时,结论还是成立.
③当四边形ABCD是梯形时,①中结论当E点为AB中点时成立,其它情况不成立不成立.

理由如下:
设S△ADE=S1,S△BCE=S2,S△DEC=S3,
梯形ABCD上底为a,下底为b面积为S,如图.
则S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
如果S△ADE+S△BCE=S△DEC,则有
| 1 |
| 2 |
| 1 |
| 2 |
如果h1=h2,则E为AB中点,如果h1≠h2,则a=b,四边形ABCD是平行四边形.
点评:解答本题要充分利用正方形、矩形,平行四边形的对边相等的性质;观察图形的底与高的关系,利用等底,等高的两个三角形面积相等,确定三角形的面积关系.

练习册系列答案
相关题目