Question

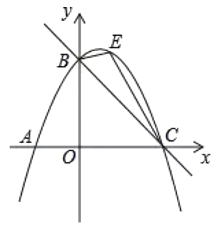
【题目】已知二次函数y=ax2+bx+c的图像经过点A(3,0),B(2,-3)C(0,-3)

（1）求此函数关系式和图像对称轴．

（2）在对称轴上是否存在一点P使得△PAB中PA=PB?若存在,求出点P坐标,若不存在,说明理由．

Answer 1

【答案】(1) y=x22x3，对称轴x=1(2) (1,1)

【解析】

（1）设二次函数的解析式为y=ax2+bx+c，把A（3，0）、B（2，-3），C（0，-3）代入，得到方程组，求出a，b，c的值，即可解答；

（2）设P（1，t），利用两点间的距离公式得到（1+1）2+t2=（1-2）2+（t+3）2，由于解得t=-1，则可判断存在一点P，使PA=PB，此时P点坐标为（1，-1）．

(1)设二次函数的解析式为y=ax2+bx+c，

把A(3,0)、B(2,3),C(0,3)代入，得，

解得：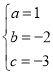

∴y=x22x3，

对称轴x===1,

(2)存在,

设P(1,t)，

∵PA=PB，

∴(1+1)2+t2=(12)2+(t+3)2，解得t=1，

∴满足条件的P点坐标为(1,1)．