��Ŀ����
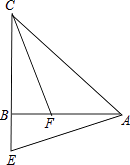
����Ŀ����ͼ���ھ���ABCD�У�AB=8k��BC=5k��kΪ��������k��0��������P��AB���ϣ���P����A��B�غϣ�����Q��R�ֱ���BC��DA���ϣ���AP��BQ��DR=3��2��1����A����ֱ��PR�ĶԳƵ�ΪA�䣬����PA�䡢RA�䡢PQ��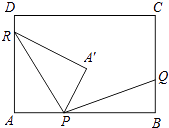
��1����k=4��PA=15�����ı���PARA�����״����
��2����DR=x����B����ֱ��PQ�ĶԳƵ�ΪB��㣮
�ټǡ�PRA������ΪS1 �� ��PQB������ΪS2 �� ��S1��S2ʱ������Ӧx��ȡֵ��Χ��S2��S1�����ֵ�����ú�k�Ĵ���ʽ��ʾ��
���ڵ�P���˶������У��жϵ�B���ܷ����A���غϣ���˵�����ɣ�
���𰸡�
��1��������
��2��
�⣺���������֪��BQ=2x��PA=3x��AR=5k��x��BP=8k��3x��
��S1=S��PRA= ![]() ARAP=
ARAP= ![]() ��5k��x��3x=��
��5k��x��3x=�� ![]() x2+
x2+ ![]() kx��
kx��
S2=S��PQB= ![]() BPBQ=
BPBQ= ![]() ��8k��3x��2x=��3x2+8kx��
��8k��3x��2x=��3x2+8kx��
��S1��S2�ɵã��� ![]() x2+
x2+ ![]() ����3x2+8kx��
����3x2+8kx��
��x��0��
��xȡֵ��ΧΪ0��x�� ![]() k��
k��
��S2��S1=�� ![]() x2+
x2+ ![]() kx=��
kx=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() k2��
k2��
�൱x= ![]() ʱ��S2��S1�����ֵ�����ֵΪ
ʱ��S2��S1�����ֵ�����ֵΪ ![]() k2��
k2��
�ڵ�B'�������A'�غϣ��������£���ͼ��
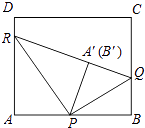
�����B'���A'�غϣ����С�APR+��A'PR+��B'PQ+��BPQ=180�㣬
�ɶԳƵ����ʿɵã���A'PR=��APR����B'PQ=��BPQ��
���APR+��BPQ= ![]() ��180��=90�㣬
��180��=90�㣬
�ɡ�A=90��ɵã���APR+��PRA=90�㣬
���PRA=��BPQ��
�֡ߡ�A=��B=90��
��Rt��PAR��Rt��QBP��
�� ![]() ����PABP=ARQB��
����PABP=ARQB��
��3x��8k��3x��=��5k��x��2x����ã�x1=0������������ȥ����x2=2k��
�֡�PA=PA'��PB=PB'=PA'��
��PA=PB��
��3x=8k��3x�����x= ![]() k��2k��
k��2k��
�ʵ�B'�������A'�غϣ�
���������⣺��1����k=4��PA=15��AP��BQ��DR=3��2��1��
��DR=5��BC=AD=20��AR=AP=15��
��A��A�����PR�Գƣ�
��RA=RA��=PA=PA�䣬
���ı���PARA�������Σ�
�ߡ�A=90�㣬
���ı���PARA���������Σ�
�ʴ�Ϊ�����Σ�
��1����֤���ı���PARA�������Σ��ٸ��ݡ�A=90�㣬�����Ƴ��ı���PARA���������Σ���2���ٷֱ����S1 �� S2 �� ����S1��S2 �� ȷ���Ա���ȡֵ��Χ���ٹ���S2��S1����x�Ķ��κ��������ݶ��κ��������ʼ��ɽ�����⣮
�ڵ�B'�������A'�غϣ����÷�֤������֤����

 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�