题目内容
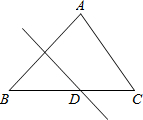（2012•鼓楼区一模）如图，△ABC中，∠ABC=45°，AC=10，对折使点B与点A重合，折痕与BC交于点D，BD：DC=4：3，则DC的长为（ ）分析：根据翻折变换的性质得出∠B=∠BAD=45°，AD=BD，进而得出∠ADB=90°，即可得出AD2+CD2=AC2，再利用BD：DC=4：3，即可求出DC的长．
解答：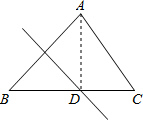
解：连接AD，
∵∠ABC=45°，对折使点B与点A重合，
∴∠B=∠BAD=45°，AD=BD，
∴∠ADB=90°，
∵BD：DC=4：3，设BD=4x，CD=3x，
∴AD2+CD2=AC2，
∵AC=10，AD=BD=4x，
∴16x2+9x2=102，
解得：x=2，
∴CD=3x=6，
故选：B．
解：连接AD，∵∠ABC=45°，对折使点B与点A重合，
∴∠B=∠BAD=45°，AD=BD，
∴∠ADB=90°，
∵BD：DC=4：3，设BD=4x，CD=3x，
∴AD2+CD2=AC2，
∵AC=10，AD=BD=4x，
∴16x2+9x2=102，
解得：x=2，
∴CD=3x=6，
故选：B．
点评：本题考查了折叠的性质，属于基础题，比较简单，掌握折叠前后对应边相等是解答本题的关键，另外同学们要学会等线段间的代换，这对以后的解题很有帮助．
练习册系列答案
相关题目
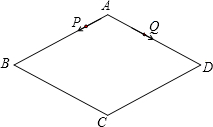/s；点Q沿折线A-D-C-B运动，速度为1.5cm/s．当一点到达终点时，另一点也随即停止运动．若点P、Q同时从点A出发，运动时间为t s．