题目内容
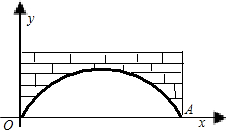 如图,有一座抛物线形的拱桥,桥下的正常水位为OA,此时水面宽为40米,水面离桥的最大高度为16米,则拱桥所在的抛物线的解析式为
如图,有一座抛物线形的拱桥,桥下的正常水位为OA,此时水面宽为40米,水面离桥的最大高度为16米,则拱桥所在的抛物线的解析式为分析:首先取水面离桥的最大高度的点C,过C作CD⊥AO于D,由垂径定理即可求得OD的长,继而求得顶点C与A的坐标,然后设拱桥所在的抛物线的解析式为:y=a(x-20)2+16,利用待定系数法即可求得拱桥所在的抛物线的解析式.
解答: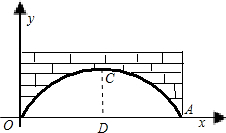 解:取水面离桥的最大高度的点C,过C作CD⊥AO于D,
解:取水面离桥的最大高度的点C,过C作CD⊥AO于D,
则OD=AD=
OA=
×40=20(米),
∴点C的坐标为(20,16),点A的坐标为(40,0),
设拱桥所在的抛物线的解析式为:y=a(x-20)2+16,
将点A代入得:400a+16=0,
解得:a=-
,
∴拱桥所在的抛物线的解析式为:y=-
(x-20)2+16.
故答案为:y=-
(x-20)2+16.
 解:取水面离桥的最大高度的点C,过C作CD⊥AO于D,
解:取水面离桥的最大高度的点C,过C作CD⊥AO于D,则OD=AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴点C的坐标为(20,16),点A的坐标为(40,0),
设拱桥所在的抛物线的解析式为:y=a(x-20)2+16,
将点A代入得:400a+16=0,
解得:a=-
| 1 |
| 25 |
∴拱桥所在的抛物线的解析式为:y=-
| 1 |
| 25 |
故答案为:y=-
| 1 |
| 25 |
点评:本题考查的是二次函数在实际生活中的应用.此题难度不大,解题的关键是理解题意,然后根据题意求得函数解析式,注意待定系数法的应用,注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


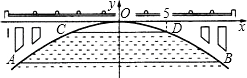 上升3米,则水面CD的宽是10米.
上升3米,则水面CD的宽是10米.