题目内容
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位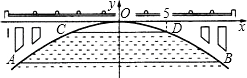 上升3米,则水面CD的宽是10米.
上升3米,则水面CD的宽是10米.(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
分析:(1)以拱桥最顶端为原点,建立直角坐标系,根据题目中所给的数据写出函数解析式.
(2)计算出本问可用两种方法求得,求x=3米时求出水面求出此时y的值,A、B点的横坐标减去y此时的值到正常水面AB的距离与3.6相比较即可得出答案.
(2)计算出本问可用两种方法求得,求x=3米时求出水面求出此时y的值,A、B点的横坐标减去y此时的值到正常水面AB的距离与3.6相比较即可得出答案.
解答:解:(1)设抛物线解析式为y=ax2,
因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,
设点B(10,n),点D(5,n+3),
n=102•a=100a,n+3=52a=25a,
即
,
解得
,
∴y=-
x2;
(2)∵货轮经过拱桥时的横坐标为x=3,
∴当x=3时,y=-
×9
∵-
-(-4)>3.6
∴在正常水位时,此船能顺利通过这座拱桥.
答:在正常水位时,此船能顺利通过这座拱桥.
因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,
设点B(10,n),点D(5,n+3),
n=102•a=100a,n+3=52a=25a,
即
|
解得
|
∴y=-
| 1 |
| 25 |
(2)∵货轮经过拱桥时的横坐标为x=3,
∴当x=3时,y=-
| 1 |
| 25 |
∵-
| 9 |
| 25 |
∴在正常水位时,此船能顺利通过这座拱桥.
答:在正常水位时,此船能顺利通过这座拱桥.
点评:此题考查了坐标系的建立,以及抛物线的性质与求值.

练习册系列答案
相关题目

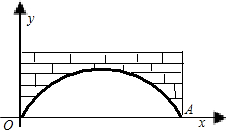 如图,有一座抛物线形的拱桥,桥下的正常水位为OA,此时水面宽为40米,水面离桥的最大高度为16米,则拱桥所在的抛物线的解析式为
如图,有一座抛物线形的拱桥,桥下的正常水位为OA,此时水面宽为40米,水面离桥的最大高度为16米,则拱桥所在的抛物线的解析式为