题目内容
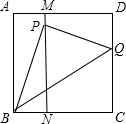如图，正方形纸片ABCD的面积为1，点M、N分别在AD、BC上，且AM=BN=| 2 | 5 |
分析：如图，作辅助线OQ⊥MN，结合已知条件可以推出NC，BP，PN，OQ，PQ，ON的长度，在直角三角形POQ中，根据勾股定理得PQ2=PO2+OQ2，通过等量转换直接求PQ2的值，即是以PQ为边长的正方形面积．
解答：解：如图，作QO⊥PN于O点，
∵正方形ABCD，AM=BN=
，
∴AB∥MN∥DC，
∴四边形ONCQ为钜形，
∴△PBN，△OPQ均为Rt△，
∵正方形纸片ABCD的面积为1，点M、N分别在AD、BC上，
∴AB=MN=DC，BC=BP=1，OQ=NC=
，
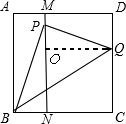
∴PN2=
，
∵PQ2=PO2+OQ2，
∴转换得：PQ2=（PN-CQ）2+（
）2，
∴化简得PQ2=PN2-2PN•CQ+CQ2+
，
∴PQ2=
，
∴PQ为边长的正方形面积为
．
∵正方形ABCD，AM=BN=
| 2 |
| 5 |
∴AB∥MN∥DC，
∴四边形ONCQ为钜形，
∴△PBN，△OPQ均为Rt△，
∵正方形纸片ABCD的面积为1，点M、N分别在AD、BC上，
∴AB=MN=DC，BC=BP=1，OQ=NC=
| 3 |
| 5 |
∴PN2=
| 21 |
| 25 |
∵PQ2=PO2+OQ2，
∴转换得：PQ2=（PN-CQ）2+（
| 3 |
| 5 |
∴化简得PQ2=PN2-2PN•CQ+CQ2+
| 9 |
| 25 |
∴PQ2=
| 3 |
| 7 |
∴PQ为边长的正方形面积为
| 3 |
| 7 |
点评：本题主要考查了全等三角形，解直角三角形的有关性和知识．本题的关键在于作好辅助线，更等量之间的转换、化简．
练习册系列答案
春雨教育同步作文系列答案
相关题目
（2013•昆山市二模）如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE=1，则EF的长为
（2012•宽城区一模）如图，正方形纸片ABCD，对角线AC、BD交于点O，折叠纸片，使AD落在BD上，点A恰好与BD上的点F重合，展开纸片后，折痕DE分别交AB、AC于点E、G，则∠AGD的度数为
已知：如图，正方形纸片ABCD的边长是4，点M、N分别在两边AB和CD上（其中点N不与点C重合），沿直线MN折叠该纸片，点B恰好落在AD边上点E处．